Durante uma avalanche, uma pedra de desliza a partir do repouso, descendo a encosta de uma montanha que tem de comprimento e de altura. O coeficiente de atrito cinético entre a pedra e a encosta é . (a) Se a energia potencial gravitacional do sistema rocha-Terra é nula na base da montanha, qual é o valor de imediatamente antes de começar a avalanche? (b) Qual é a energia transformada em energia térmica durante a avalanche? (c) Qual é a energia cinética da pedra ao chegar à base da montanha? (d) Qual é a velocidade da pedra nesse instante?
Passo 1
Fala galerinha, tudo certo? Como são muitos itens pra gente fazer, vamos devagarzinho fazendo um passo de cada vez.
- Considerando o eixo de referência localizado na base da montanha, com o sentido positivo de para cima, podemos calcular a energia potencial inicial da seguinte forma:
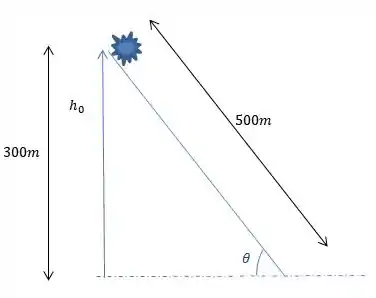
Passo 2
b) Como e , temos:
Onde:
é a força de atrito.
é a força normal
é a variação da energia térmica, e é a distância percorrida, temos:
Lembrando que nesse caso a gente tá falando de plano inclinado e a força normal nesses casos é dada por:
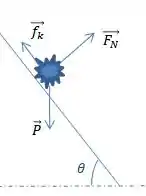
Logo.
O valor de e da distância podem ser encontrados da seguinte forma:
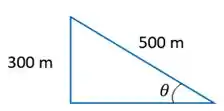
Enquanto a distância percorrida pela pedra vai ser o próprio comprimento da montanha, né!
E por fim, encontrando a nossa variação de energia térmica:
Passo 3
c) Com o nosso teorema da conservação da energia a gente pode isolar a energia cinética final.
Perceba que não há pois a rocha sai do repouso no topo da montanha, e não há pois na base da montanha a rocha estará na altura do nível de referência.
E substituindo os valores encontrados, a gente pode encontrar a nossa energia cinética final.
Passo 4
d) Para encontrar a velocidade final agora é fácil, já que temos o valor da energia cinética final:
E substituindo os valores que temos:
E realizando essa conta, encontramos que:
Que é a velocidade da nossa pedra ao chegar no topo da montanha!
Resposta
a)
b)
c)
d)