Enunciado
Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 69
Encontre o potencial e o campo elétrico em pontos no eixo de um disco de um disco de raio R que contém uma carga cr por unidade de área. [Dica: divida o disco em anéis e adicione as eras de todos os anéis.]
Passo 1
Opaa tudo certo?
Vamos lá para mais um problema bem legal ein!
Passo 2
Vou desenhar pra gente entender melhor o problema, beleza? Vamos levar em consideração a dica que o autor fala pra gente, então vamos dividir o anel em três e somar as contribuições de cada um
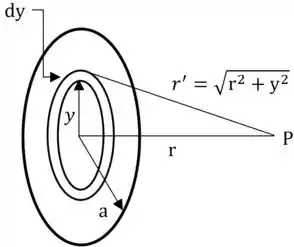
Passo 3
O pedaço infinitésimo de carga é dado por
Passo 4
O potencial é calculado por
Integrando dos dois lados da equação temos:
Passo 5
O campo elétrico é dado por