Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 72

Com um fio de carga λ por unidade de comprimento de um quadrado é formado lado L. Calcule o campo elétrico e potencial em pontos localizados em a perpendicular ao quadrado por seu Centro.

Passo 1

Eaii tudo bem?

Vamos lá para mais um problema bem legal ein!

Passo 2

Vou fazer um desenho do que o problema pede pra ficar mais claro pra gente o que tem que ser feito beleza?

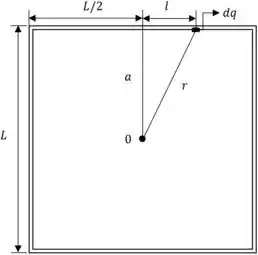
Onde a = L / 2 e r = L 2 + a 2

Passo 3

O potencial é dado por

d V 0 1 = 1 4 π ε 0 ⋅ d q r = 1 4 π ε 0 ⋅ λ d l r → d V 0 1 = λ 4 π ε 0 ⋅ d l L 2 + a 2

Podemos integrar dos dois lados da equação:

V 0 1 = λ 4 π ε 0 ∫ - L / 2 L / 2 d l L 2 + a 2 = λ 4 π ε 0 ⋅ ln ⁡ L + L 2 + a 2 - L / 2 L / 2

Como temos a = L / 2

V 0 1 = λ 4 π ε 0 ⋅ ln ⁡ L 2 + 2 L 2 2 - ln ⁡ - L 2 + L 2 2

Fazendo manipulações, podemos concluir que

V 0 1 = 2 λ 4 π ε 0 ln ⁡ 2 + 1

Passo 4

O campo elétrico então pode ser calculado por

E = - d V d x

Resposta

V 0 1 = 2 λ 4 π ε 0 ln ⁡ 2 + 1

Ver Outros Exercícios desse livro