Enquanto as bolas descem um plano inclinado rolando, Galileu observa que a bola rola um cúbito* (a distância do cotovelo até a ponta dos dedos) enquanto ele conta até 10. Quão longe a bola terá rolado a partir de seu ponto inicial quando ele tiver contado até 20?

A gente sabe que a bola está rolando em um plano inclinado que faz um ângulo com o eixo horizontal, e a bola rola em um tempo de .

Na Figura 1 vemos uma representação do sistema junto com o sistema de coordenados considerado positivo. Na figura 2 temos a representação de forças atuando na bola.

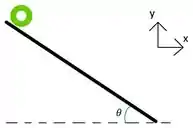
Figura 1: Representação sistema. Figura 2: Forças atuando na bola.

Durante o movimento, a aceleração gravitacional será e, já que a bola começa a rolar do seu ponto de repouso, sua velocidade inicial é . Ela percorre o eixo y enquanto ele conta até . Faremos uma conta de 10 ser igual a segundos, e uma conta de 20 ser igual a segundos.

Usando a segunda equação do movimento cinemático, que é dada por

Onde é a distância que a bola viaja, é a velocidade inicial, é a aceleração da bola e é o tempo do movimento.

Agora podemos substituir os valores obtidos na equação, tendo:

Agora, podemos achar a distância em . Aplicando a segunda equação do movimento cinemático através da gravidade , temos: