Na equação obtida no problema 1, considere o potencial núcleon-núcleon como sendo um poço de potencial quadrado de raio e profundidade , como indica a figura 17-2.
B – Mostre por substituição que a solução geral da equação obtida é
C – Calcule e em termos de e da energia de ligação de dêuteron .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
A – Na ordem de mostrar que as soluções para da equação de Schroedinger para um dêuteron na camada de ligação, com isso temos que
Aqui, é a massa reduzida do sistema, é o potencial da profundidade, como uma função do raio. As soluções gerais para a equação acima são as seguintes
Bem, depois dessa introdução, vamos começar diferente, vamos primeiro fazer um gráfico do potencial para termos uma facilidade acerca de referência, com isso temos o seguinte gráfico
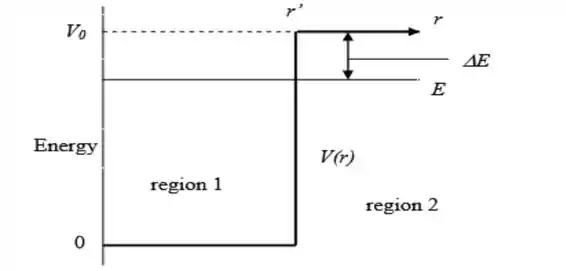
Para a região 1, vamos inserir 0 para , com isso vamos ter
Logo, temos que
E para a região 2, temos a seguinte configuração, dessa vez vamos utilizar o no lugar de
Passo 2
B – Agora é mostrar as soluções, o primeiro é reescrever a energia de ligação nos seguintes termos, para a região 1, a relação é igual a , então usando esta situação para o e rearranjando a equação numa equação mais padrão, temos
Resposta
Respostas nos passos