Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 14.Problemas - Ex. 26
Uma esfera de massa M é suportada por uma corda que passa sobre uma roldana leve na extremidade de uma barra horizontal de comprimento L (Fig. P14.25). A corda forma um ângulo u com a barra. A frequência fundamental de ondas estacionárias na porção da corda acima da barra é f. Encontre a massa da porção da corda acima da barra.
Passo 1
Faaalaaaaaa papitooooo, rs!
Tudo bem galera??
Bora láa!!
Para a resolução, vamos considerar a seguinte equação:
Para calcular o valor da velocidade , vamos considerar o esquema representado a
Seguir. Note que, acima da haste, a corda tem apenas dois nodos (no estado fundamental) nos pontos A e B, e um antinodo em .
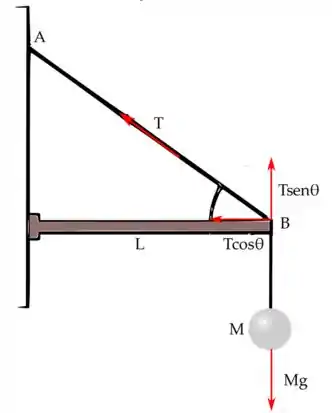
Partindo da decomposição de forças representada na figura, temos que :
Então
A velocidade da onda na corda (v) será igual a:
Deste modo
Passo 2
Iremos elevar ambos os lados ao quadrado e rearranjarmos a equação, temos:
Logo
Passo 3
Agora que já conhecemos a expressão para efetuar o cálculo de é possível notar que ainda precisamos calcular o valor da tensão (T). Tenha em mente que para que o sistema se mantenha imóvel, a seguinte condição deve ser satisfeita.
Para calcular a tensão, podemos utilizar a terceira lei de Newton (vamos observar a decomposição de forças apresentada na figura anterior)
Onde
Agora ficamos com a seguinte expressão para o cálculo da massa da corda:
Resposta
Vide a explicação.