Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.6 - Ex. 32
Um esquiador de massa é puxado para cima em uma encosta coberta de neve, a uma velocidade escalar constante, pelo cabo de um reboque que está paralelo ao solo. O solo tem inclinação de de baixo para cima, formando um ângulo de acima da horizontal, e o atrito é desprezível.
- Faça um diagrama do corpo livre para o esquiador.
- Calcule a tensão no cabo do reboque.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um esquiador de massa é puxado para cima em uma encosta coberta de neve, a uma velocidade escalar constante, pelo cabo de um reboque que está paralelo ao solo.
Bom... se a velocidade é constante, então a aceleração é zero.
Pela segunda Lei de Newton, temos que a força resultante é dada por:
Como a aceleração é zero, então a força resultante é zero!!
Mas vamos continuar com o enunciado...
O enunciado nos diz ainda que a solo tem inclinação de de baixo para cima, formando um ângulo de acima da horizontal, e o atrito é desprezível.
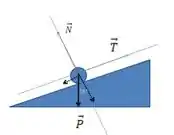
Queremos fazer um diagrama de corpo livre, ou seja, fazer uma figura mostrando tooodas as forças (com direção e sentido) que estão atuando no esquiador.
Com esse diagrama, devemos calcular a tensão no cabo.
Agora bora lá!! 😉
Passo 2
Sobre esse esquiador estão agindo a força normal (perpendicular à superfície de contato, aontando para cima; é reação ao contato dele com o solo) e o peso (vertical para baixo, exercida pela Terra).
E como ele está sendo puxado por um cabo, devemos levar em conta a tensão no fio. Levando em consideração essas forças, temos o diagrama:
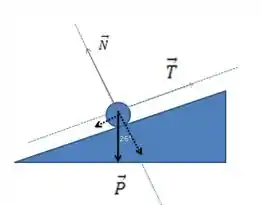
A força normal está em vermelho, a tensão em verde e o peso em preto.
Como temos uma superfície inclinada, podemos decompor a força peso em componentes vertical e horizontal:
Note que ambas componentes são negativas.
Passo 3
O problema nos diz que o esquiador sobe a encosta com velocidade constante, logo não há força resultante agindo sobre ele pois a aceleração é zero!!
Sendo assim todas as forças verticais e horizontais estão equilibradas.
A tensão está na direção horizontal e é contrabalançada com a componente horizontal do peso. E
quacionando as forças horizontais temos:
Resposta
