Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Uma esquiadora que pesa passa pelo alto de um morro circular sem atrito de raio (Fig. 8-60). Suponha que os efeitos da resistência do ar sejam desprezíveis. Na subida, a esquiadora passa pelo ponto , onde o ângulo é , com uma velocidade de . (a) Qual é a velocidade da esquiadora no alto do morro (ponto ) se ela esquia sem usar os bastões? (b) Qual a menor velocidade que a esquiadora deve ter em para conseguir chegar ao alto do monte? (c) As respostas dos itens anteriores serão maiores, menores ou iguais se o peso da esquiadora for aumentado para ?
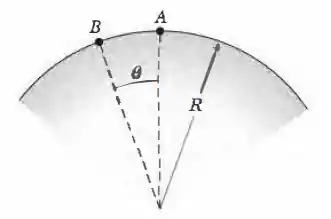
Figura 8-60 Problema 74.
Passo 1
a) Vamos aplicar a lei da conservação de energia nos pontos e .
Em , ela tem tanto energia cinética (porque está se movendo) quanto potencial gravitacional (por conta da altura dela). Em , ela tem gravitacional também e queremos encontrar sua velocidade. Então, nossa conservação de energia fica assim:
Obs.: Toma-se o centro da circunferência como referência para a energia potencial gravitacional
Passo 2
- No ponto B:
Onde é encontrado pela imagem abaixo
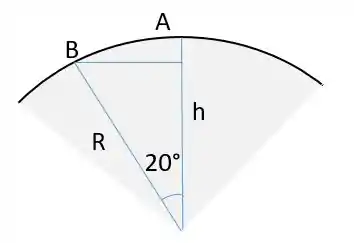
A energia potencial gravitacional fica, então:
- No ponto
Substituindo os valores encontrados na equação da conservação:
Vamos mexer um pouquinho nela:
Isolando o :
Substituindo os valores dados:
Passo 3
b) Para que a esquiadora chegue pelo menos ao topo do monte, sua velocidade deve ser nula nesse ponto, logo, agora, em não teremos energia cinética:
Substituindo os valores:
Passo 4
c) Pela lei da conservação de energia
Logo, verifica-se que nada aqui, nem mesmo as velocidades dependem da massa e, portanto, não dependem do peso. Ou seja as velocidades permanecem iguais.
Resposta
a)
b)
c) as velocidades permanecem iguais