Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 13.Problemas - Ex. 51

A excentricidade e e o semieixo maior a das órbitas de alguns planetas, estão tabelados a seguir. (Lembre-se de que 1 A . u = 1,495 × 10 11   m .)

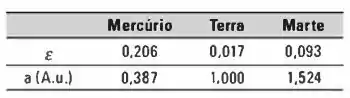
Para cada um desses planetas calcule: (a) a distância de máxima aproximação do Sol, (b) a distância de máximo afastamento do Sol, (c) a energia total do movimento de translação, (d) o momento angular, (e) o período de revolução, (f) a velocidade no afélio e no periélio.

Passo 1

E aí, beleza?? Podemos determinar r ( θ ) com:

p 1 1 + e + 1 1 - e = 2 p 1 - e 2 = 2 a ∴ p = a 1 - e 2

Portanto:

r θ = a 1 - e 2 1 + e cos ⁡ θ

Assim, as distâncias máxima e mínima são:

r p e r = a 1 - e

r a f = a 1 + e

Passo 2

A energia total é:

E = - G M m 2 a

Assim, podemos calculas as velocidades no afélio e no periélio:

E = - G M m 2 a = 1 2 m v a f 2 - G M m a 1 + e ∴ v a f = G M a 1 - e 1 + e

1 2 m v p e r 2 = G M m a 1 - e - G M m 2 a ∴ v p e r = G M a 1 + e 1 - e

Passo 3

Para o momento angular, vem:

L = m r a f v a f = m a 1 + e G M a 1 - e 1 + e

Portanto:

L = m G M a 1 - e 2

E, para o período, da terceira lei de Kepler:

T 2 a 3 = 4 π 2 G M ∴ T = 2 π a a G M

Portanto, numericamente, temos (respostas):

Resposta

Mercúrio:

(a)

r p e r = 4,59 × 10 10 m

(b)

r a f = 6,98 × 10 10 m

(c)

E = - 4 × 10 39 J    

(d)

L = 9,95 × 10 38 m 2 k g / s

(e)

T = 7,6 × 10 6 s

(f)

v p e r = 66,1   k m / s

v a f = 43,5   k m / s

Terra:

(a)

r p e r = 1,47 × 10 11 m

(b)

r a f = 1,52 × 10 11 m

(c)

E = - 2,64 × 10 32 J

(d)

L = 2,718 × 10 40 m 2   k g / s

(e)

T = 3,16 × 10 7 s

(f)

v p e r = 3 0 , 2 k m / s

v a f = 2 1 , 9   k m / s

Marte:

(a)

r p e r = 2,07 × 10 12 m

(b)

r a f = 2,49 × 10 12 m

(c)

E = - 1,85 × 10 31 J

(d)

L = 3,445 × 10 39 m 2 k g / s

(e)

T = 5,94 × 10 7 s

(f)

v p e r = 2,17   k m / s

v a f = 2,64   k m / s

Ver Outros Exercícios desse livro