Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 19.Exercício - Ex. 23
Em uma experiência para simular as condições no interior de um motor de automóvel, de calor são transferidos para de ar contido no interior de um cilindro com volume igual a . Inicialmente, o nitrogênio está a uma pressão de à temperatura de .
- Se o volume do cilindro é mantido constante, qual é a temperatura final do ar? Suponha que o ar seja constituído essencialmente de nitrogênio e use os dados da Tabela 19.1, mesmo que a pressão não seja baixa. Faça um diagrama para esse processo.
- Calcule a temperatura final do ar supondo que o volume do cilindro possa aumentar enquanto a pressão permanece constante. Faça um desenho do diagrama para esse processo.
Passo 1
Olá, tudo bem? Vou ajudar você nessa aqui!
Borá lá?
Letra a)
Os dados que o problema nos trás são:
Como o processo é a volume constante, podemos por meio da fórmula encontrar a variação de temperatura. E já que foi dada a temperatura inicial, encontrar a temperatura final é mamão com açúcar =) Vamos começar?
Na tabela dos calores específicos do livro texto temos que , daí o valor de é:
Daí a temperatura final vai ser:
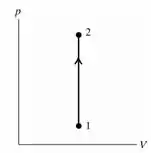
Agora vamos ao desenho do diagrama. Como se trata de um processo a volume constante, temos que o desenho será uma reta vertical indo do estado para o estado :
Passo 2
Letra b)
Agora o processo é a pressão constante. A ideia aqui vai ser bem semelhante: vamos usar a fórmula do calor à pressão constante para determinar o valor da variação de temperatura e assim determinar a temperatura final do sistema. Bora lá?
Da mesma tabela temos que o valor de é , daí a variação de temperatura é:
Daí a temperatura final vai ser:
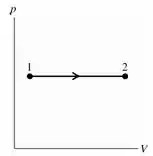
Agora vamos ao desenho do diagrama. Como se trata de um processo à pressão constante, temos que o desenho será uma reta horizontal indo do estado para o estado :
Resposta
