(a) Faça o gráfico dos potenciais V‘(r) definido no problema 16, para o átomo de argônio para l = 0 e l = 1, adicionando os potenciais centrífugos correspondentes ao V(r) obtido no problema 13. (b) Desenhe também o nível de energia E_2. (c) Mostre os limites do movimento clássico, quando E2 > V‘(r).(d) Compare esses limites com as densidades de probabilidades radiais da figura 9-10, para n = 2, l = 0 e n = 2, l = l.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de física quântica?!
Passo 2
Para o átomo de argônio , não existe o momento angular, então o potencial não muda
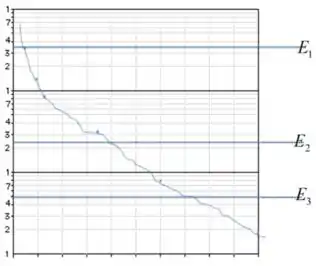
Passo 3
Classicamente, os elétrons tem que estar em , isso está de acordo com a densidade de probabilidade radial.
Para , o potencial tem um termo adicional de:
E
Os valores do novo potencial estão na tabela abaixo:

Passo 4
O desenho é:
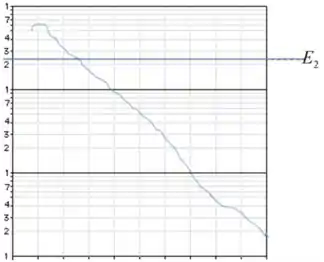
Classicamente, o elétron tem que estar em e não pode chegar perto de , isso concorda com a densidade de probabilidade radial.
Resposta
Ei, a resposta está no passo a passo :)