As faces de um tetraedro regular são triângulos equiláteros de lado . Determine, por métodos vetoriais, o ângulo que cada lado faz com a face oposta e a distância entre um vértice e a face oposta.
Passo 1
E aí, beleza?? Vamos posicionar o tetraedro de modo que sua base esteja distribuída segundo a figura abaixo:
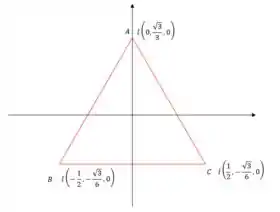
Note que nesse sistema o outro vértice está em , em que é determinado por:
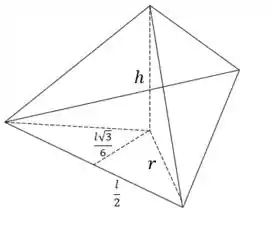
Nessa figura, temos:
Logo:
Ou seja, o outro vértice está em .
Passo 2
Considerando que agora localizamos os pontos do tetraedro, a questão fica mais simples agora. Considere a seguinte figura para basear o restante da questão:
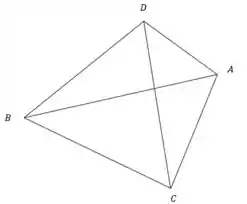
Assim, vamos calcular o ângulo que o lado faz com a face . O vetor normal a essa face é dado pelo produto vetorial:
Portanto, o produto escalar nos fornece:
Logo:
Passo 3
Agora, vamos calcular a distância do ponto ao plano gerado por e e que passa por . Para isso, vamos usar o resultado na resolução do exercício . Lá, foi demonstrado que a distância pode ser obtida com:
Onde é um vetor perpendicular ao plano, ou seja:
Portanto:
Substituindo os valores, temos:
Resposta
Olhar passo a passo