Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 70
Na Fig. 35-44, um feixe de luz com um comprimento de onda de incide perpendicularmente na placa superior de um par de placas de vidro que estão em contato na extremidade esquerda. O ar entre as placas se comporta como um filme fino e um abservador situado acima das placas vê uma figura de interferência. Inicialmente, existem uma franja escura na extremidade esquerda, uma franja clara na extremidade direita e nove franjas escuras fora das extremidades. Quando as placas são aproximadas a uma taxa constante, a franja do lado direito muda de clara para escura a cada . (a) A que taxa a distância entre as extremidades das placas na extremidade direita está variando? (b) Qual é o valor da variação no momento em que existem franjas escuras nas duas extremidades e cinco franjas escuras fora das extremidades?
Passo 1
O problema fala sobre um filme fino de ar em formato de cunha, como mostra a figura:
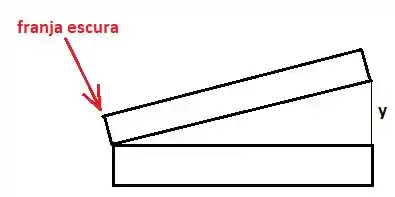
Como o filme de ar está entre as placas de vidro, a primeira reflexão ocorre na interface entre o vidro e o ar, de modo que não inversão de fase, enquanto a segunda ocorre do ar pro vidro, ocorrendo inversão. Como em um reflexão a fase inverte e na outra não, devemos adicionar na defasagem:
Como no problema vamos analisar o que acontece na extremidade direita, a diferença de caminho será sempre :
Note que aqui não precisei usar algum índice de refração pois o filme é composto de ar em que . Assim, para que haja interferência:
Se for par, ela será construtiva, se for ímpar ela será destrutiva. Assim,
Sabemos que na extremidade esquerda . Assim, temos que a primeira franja escura corresponde a .
Passo 2
Vamos analisar o item (a). Queremos saber a taxa com que varia quando a cada a franja do lado direito muda de clara para escura. Sabemos que
Assim,
Quando a franja muda de clara para escura, temos que (o sinal negativo significa q distância está diminuindo). Assim,
Portanto,
Em módulo:
Passo 3
Agora vamos fazer o item (b). Na situação inicial, a extremidade da direita tem uma franja na extremidade direita com nove franjas escuras entre as extremidades. Assim, ao todo (contando com extremidade esquerda), temos 10 franjas escuras, o que seria equivalente a . Assim, a franja clara seguinte seria :
Na situação final, a extremidade direita tem um franja escura com cinco franjas escuras no meio, assim, ela será a sétima franja escura: . Portanto,
Desta forma,
Em módulo,