Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 72
Na Fig. 35-44, um feixe de luz monocromática incide perpendicularmente em duas placas de vidro mantidas em contato em uma das extremidades para criar uma cunha de ar. Um observador que olha para baixo através da placa superior vê franjas escuras. Quando o ar entre as placas é removido, apenas franjas são vistas. Use esses dados para calcular o índice de refração do ar com seis algarismos significativos.
Passo 1
O problema fala sobre um filme fino de ar em formato de cunha, como mostra a figura:
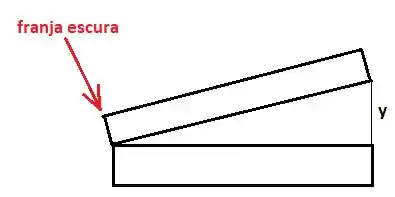
Como o filme de ar está entre as laminas, a primeira reflexão ocorre na interface entre o vidro e o ar, de modo que não inversão de fase, enquanto a segunda ocorre do ar pro vidro, ocorrendo inversão. Como em um reflexão a fase inverte e na outra não, devemos adicionar na defasagem:
A diferença de caminho será :
Usei também que , onde é o comprimento de onda no vácuo e é o índice de refração do ar. Aqui, diferentemente de outros problemas, não vamos considerar , pois isso é uma aproximação. O índice de refração só exatamente igual a no vácuo!
Para que haja interferência:
Se for par, ela será construtiva, se for ímpar ela será destrutiva. Assim,
Sabemos que na extremidade esquerda . Assim, temos que a primeira franja escura corresponde a .
Passo 2
Quando a cunha é preenchida com ar, temos franjas escuras. Isso significa que a franja escura da extremidade direita é dada por . Assim
Por outro lado, quando retiramos o ar da cunha, uma das franjas é perdida: . Além disso, agora o índice de refração é :
Igualando as duas expressões:
Esse é o índice de refração do ar com seis algarismos significiativos!