Na Fig. 35-44, duas lâminas de microscópio estão em contato em uma das extremidades e separadas na outra. Quando uma luz com um comprimento de onda de incide verticalmente na lâmina superior, um observador situado acima das lâminas vê uma figura de interferência na qual as franjas escuras estão separadas por uma distância de . Qual o ângulo entre as lâminas?

O problema fala sobre um filme fino de ar em formato de cunha, como mostra a figura:

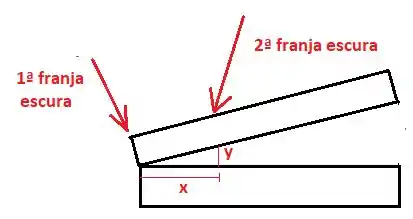
Como o filme de ar está entre as laminas, a primeira reflexão ocorre na interface entre o vidro e o ar, de modo que não inversão de fase, enquanto a segunda ocorre do ar pro vidro, ocorrendo inversão. Como em um reflexão a fase inverte e na outra não, devemos adicionar na defasagem:

A diferença de caminho será :

Note que aqui não precisei usar algum índice de refração pois o filme é composto de ar em que . Assim, para que haja interferência:

Se for par, ela será construtiva, se for ímpar ela será destrutiva. Assim,

Sabemos que na extremidade esquerda . Assim, temos que a primeira franja escura corresponde a .