Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
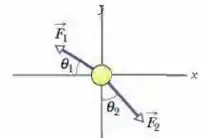
A Fig. 5-39 mostra uma vista superior de um disco de sobre uma mesa sem atrito e duas das três forças que agem sobre o disco. A força tem um módulo de e um ângulo . A força tem um módulo de e um ângulo . Em termos dos vetores unitários, qual é a terceira força se o disco (a) está em repouso, (b) tem uma velocidade constante e (c) tem uma velocidade variável , onde é o tempo?
Passo 1
Show de bolinhas galera, pra gente iniciar essa questão precisamos ter em mente que a força resultante que age sobre um corpo é igual a soma de todas as forças que atuam no mesmo, e está relacionada à aceleração pela definição da segunda lei de Newton, tal que:
Para facilitar a resolução desta questão, podemos aplicar a segunda lei de Newton para cada componente, assim:
Além disso, precisamos ter em mente que a força resultante está relacionado somente com a aceleração do corpo. Se a velocidade é nula ou é constante diferente de zero, não importa, o que importa é que em ambos os casos a aceleração tem que ser nula e, portanto, a força resultante precisa também ser nula.
Nesta questão foi dado o módulo das duas forças ( e ), os ângulos dessas forças e nos pede qual o valor da terceira força no caso do disco está em repouso, ter uma velocidade constante e uma velocidade variável dada.
Passo 2
Para iniciar, vamos escrever as forças em termos de suas componentes:
Agora para :
Enquanto pode ser expressa como:
Escrevendo a soma vetorial:
Fazendo a combinação das componentes, eixo por eixo:
Passo 3
Iradoso, agora com as equações da segunda lei de Newton em cada componente, podemos substituir os valores interpretados pela questão. Primeiro vamos lembrar que se a velocidade é nula ou ela é diferente de zero, mas é constante, então a soma vetorial deve ser nula. Assim, reescrevendo as equações acima para o eixo :
Então, isolando :
Agora, para o eixo :
Isolando :
Portanto:
Passo 4
Por fim, se a velocidade varia, então a aceleração é diferente de zero, show? Então, precisamos encontrar essa aceleração, para isso, devemos lembrar que:
Portanto:
Uma vez definido a aceleração, podemos substituir nas equações, sabendo que , então para o eixo :
Isolando :
De maneira análoga para o eixo :
Isolando :
Assim:
Resposta
- ;
- ;
- .