Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
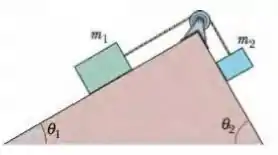
A Fig. 5-60 mostra uma caixa de dinheiro sujo (massa ) sobre um plano inclinado sem atrito de ângulo . A caixa está ligada por uma corda de massa desprezível a uma caixa de dinheiro lavado (massa ) situada sobre um plano inclinado sem atrito de ângulo . A polia não tem atrito e a massa é desprezível. Qual é a tensão da corda?
Passo 1
Vamos iniciar esta questão fazendo o esboço das forças aplicadas em cada bloco.
Lembrando que, como os blocos se movem em conjunto, o módulo da aceleração de cada bloco é a mesma.
A tração também terá o mesmo módulo tendo em vista que a polia é ideal:
A partir dessa ilustração vamos escrever a segunda lei de Newton para cada um dos blocos, Não sabemos qual bloco vai subir ou descer o plano inclinado por isso, vamos supor que o bloco está subindo o plano inclinado e o bloco 2 descendo , caso essa afirmação seja falsa, o módulo da aceleração que encontraremos será negativo e saberemos que se trata do caso contrário.
Passo 2
Sabemos que os dois blocos têm em comum duas coisas: a aceleração e a tração. Vamos trabalhar em cima dessas informações.
Aplicando a segunda lei de Newton para o bloco para o eixo temos:
Vamos tentar encontrar uma equação que relacione a tensão com a aceleração que sabemos que são comuns aos dois blocos.
Podemos colocar a aceleração em função da tensão :
Vamos guardar essa equação ()por enquanto.
Passo 3
Aplicando agora a segunda lei de Newton para o bloco :
Podemos substituir a aceleração pela que achamos anteriormente:
Agora só precisamos substituir o valor das massas que foi dado no enunciado e isolar o T para descobrir seu valor:
Isolando o :