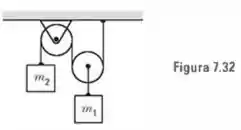
Na Fig. , os corpos estão ligados por um fio conforme indicado. Admitindo que as polias sejam lisas, calcule a aceleração dos corpos e a tensão no fio. Apresente, primeiro uma solução algébrica e, em seguida, aplique ao caso e .
Passo 1
E aí, beleza?? Nessa questão, temos dois fios envolvidos e uma polia móvel. Seja a tensão no fio ligado ao bloco e a tensão no fio ligado ao bloco , então vem:
Além disso, seja a aceleração do bloco e a aceleração do bloco , vem:
Passo 2
Portanto, a segunda lei de Newton fornece:
Multiplicado a segunda equação por , vem:
Somando:
Logo:
Passo 3
Para as tensões: