Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Na Fig. 7-32, uma força horizontal de módulo é aplicada a um livro de psicologia de enquanto o livro escorrega por uma distância ao longo de uma rampa de inclinação , subindo sem atrito . (a) Neste deslocamento, qual é o trabalho total realizado sobre o livro por , pela força gravitacional e pela força normal? (b) Se o livro tem energia cinética nula no início do deslocamento, qual é sua energia cinética final?
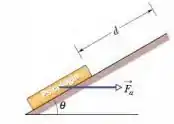
Passo 1
Bom pessoal , definindo o eixo como o eixo paraleto ao plano da rampa , nós temos que o trabalho realizado pelas forças que atuam no livro pode ser obtido através da relação :
Reparem que o eixo foi desconsiderado pois não há movimento em sua direção. Dessa forma, os trabalhos da força normal e da componente da força gravitacional são nulos!! Pois não há deslocamento por essas forças. Assim como não haverá trabalho realizado pela componente de .
Olhando para o eixo , podemos esperar que as componentes da força e da força gravitacional estejam em sentidos contrários. Logo, pela segunda Lei de Newton, a força resultante em será:
Como , temos que :
Sendo assim :
Passo 2
Então galera, se o livro, inicialmente está em repouso, sua energia cinética inicial é nula, certo? Além disso, podemos usar o teorema trabalho-energia cinética para saber qual a energia cinética final do livro:
Como a energia inicial é :
Logo, a energia cinética final será igual ao trabalho total realizado pelas forças no deslocamento do livro, que já calculamos na letra anterior:
Prontinho!! 😊