Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
A ponte de Harvard, que atravessa o rio Charles, ligando Cambridge a Boston, tem um comprimento de 364,4 smoots mais uma orelha. A unidade chamada de smoot tem como padrão a altura de Oliver Reed Smoot, Jr., classe de 1962, que foi carregado ou arrastado pela ponte para que outros membros da sociedade estudantil Lambda Chi Alpha pudessem marcar (com tinta) comprimentos de 1 smoot ao longo da ponte. As marcas têm sido refeitas semestralmente por membros da sociedade, normalmente em horários de pico, para que a polícia não possa interferir facilmente . (Inicialmente, os policiais talvez tenham se ressentido do fato de que o smoot não era uma unidade fundamental do SI, mas hoje parecem conforma-
dos com a brincadeira.) A Fig. 1-4 mostra três segmentos de reta paralelos medidos em smoots (S), willies (Y), e zeldas (Z). Quanto vale uma distância de 50,0 smoots (a) em willies e (b) em zeldas?
Passo 1
Show de bolinhas galerinha, bora lá dar uma olhadinha nesse exercício.
Se liga só, o nosso objetivo neste exercício é obter uma relação entre as distâncias , e . Pra isso, podemos observar que a figura ilustrada no problema nos passa algumas informações sobre essas distâncias.
Por exemplo, os segmentos de reta medidos em e partem do mesmo ponto zero e percorrem uma mesma distância:
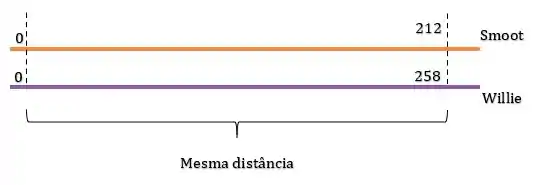
Isso quer dizer que se a gente pegar cada escala, teremos que:
Logo:
Com isso teremos que será escrito como:
Passo 2
Bom galerinha, esse item é um pouco diferente do anterior. Porque saca só, agora a distância equivalente entre as duas unidades não partem mais da origem, temos que elas estão dispostas como:
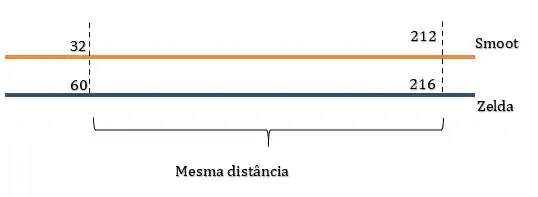
Dessa forma, podemos expressar a mesma distância em função dos intervalos que elas descrevem, como:
Resolvendo isso aí, ficamos com:
Tal que:
Com isso chegamos na equação:
Resposta
- 43,3