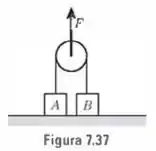
Na Fig. , as massas de e são e , respectivamente. Se uma força para cima é a aplicada na polia, calcule as acelerações de e como funções do tempo. O que acontece após alcançar a polia?
Passo 1
E aí, beleza?? No referencial da polia, temos que o corpo possui aceleração , enquanto o corpo possui aceleração . Nesse referencial, essas acelerações devem ser iguais, portanto:
Esse vínculo geométrico não será utilizado na resolução do problema, mas já fica de dica pra alguma questão parecida que você encontrar no futuro 😉. Note que no capo em que a polia está fixa, e retornamos a
Passo 2
Escrevendo a segunda lei de Newton, temos:
Portanto:
Passo 3
Numericamente, vem:
Após a colisão de com a polia, haverá uma inversão na velocidade dos blocos, que pode ser modelada com perda de energia. Eventualmente, voltaria a colidir com a polia outras vezes.