Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
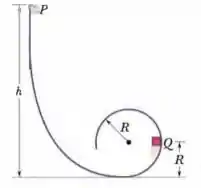
Na Fig. 8-31, um pequeno bloco de massa pode deslizar em uma pista sem atrito que forma um loop de raio . O bloco é liberado a partir do repouso no ponto , a uma altura acima do ponto mais baixo do loop. Qual é o trabalho realizado sobre o bloco pela força gravitacional quando o bloco se desloca do ponto para (a) o ponto e (b) o ponto mais alto do loop? Se a energia potencial gravitacional do sistema bloco-Terra é tomada como zero no ponto mais baixo do loop, qual é a energia potencial quando o bloco se encontra (c) no ponto , (d) no ponto e (e) no ponto mais alto do loop? (f) Se, em vez de ser simplesmente liberado, o bloco recebe uma velocidade inicial para baixo ao longo da pista, as respostas dos itens de (a) e (e) aumentam, diminuem ou permanecem as mesmas?
Passo 1
Como a força gravitacional é uma força conservativa, podemos usar o seguinte teorema para calcular o trabalho realizado por ela:
Assim, escrevendo a equação da energia potencial gravitacional, temos:
Vamos perceber, também, que o raio foi dado em , para transformar para o SI, vamos usar um fator multiplicativo de . Assim:
Para esta questão, vamos considerar que o seja no ponto mais baixo.
Passo 2
Calculando a variação da altura entre o ponto e o ponto , temos:
Assim, o trabalho realizado pelo peso entre esses pontos é:
Passo 3
Calculando a variação da altura entre o ponto e o ponto mais alto do loop, temos:
Assim, o trabalho realizado pelo peso entre esses pontos é:
Passo 4
Continuando considerando o ponto mais baixo do loop como , então a energia potencial para o bloco no ponto é:
Passo 5
De maneira análoga, a energia potencial para o ponto :
Passo 6
E para o ponto mais alto do loop:
Passo 7
Para resolver esta questão, não usamos a velocidade em nenhum momento. Os cálculos dependeram apenas da massa, da aceleração da gravidade e da variação da altura, portanto, a velocidade não mudará nenhum resultado.
Resposta
- ;
- ;
- ;
- ;
- ;
- .