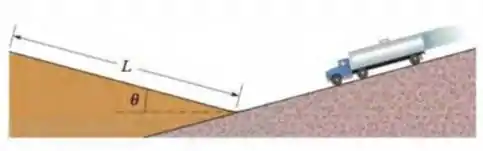
Na Fig. 8-33, um caminhão perdeu os freios quando estava descendo uma ladeira a e o motorista dirigiu o veículo para uma rampa de emergência sem atrito com uma inclinação . A massa do caminhão é . (a) Qual é o menor comprimento que a rampa deve ter para que o caminhão pare (momentaneamente) antes de chegar ao final? (Suponha que o caminhão pode ser tratado como uma partícula e justifique essa suposição.) O comprimento mínimo aumenta, diminui ou permanece o mesmo (b) se a massa do caminhão for menor e (c) se a velocidade for menor?

Quando o caminhão passa a se deslocar na rampa de energia, somente a força gravitacional realiza trabalho, tendo em vista que não há atrito e a força normal atua perpendicular ao deslocamento. Assim, como o peso é uma força conservativa, podemos aplicar a conservação da energia mecânica, assim considerando o ponto inicial da ladeira de emergência como , então:

No ponto inicial, a altura é zero, portanto a energia potencial gravitacional é nula e, quando o caminhão alcança a altura máxima, a velocidade é nula e, portanto, a energia cinética é zero. Assim:

Isolando :

Substituindo os valores:

Obs: foi usado um fator de multiplicando a velocidade para fazer a conversão de para .