Na Fig. 8-49, um bloco desliza para baixo em um plano inclinado. Enquanto se move do ponto para o ponto , que estão separados por uma distância de , uma força , com módulo de e dirigida para baixo ao longo do plano inclinado, age sobre o bloco. O módulo da força de atrito que age sobre o bloco é . Se a energia cinética do bloco aumenta de entre e , qual é o trabalho realizado pela força gravitacional sobre o bloco enquanto ele se move de até ?
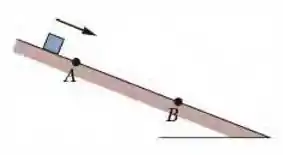
Figura 8-49 Problema 48
Passo 1
Fala galerinha tudo certo? Vamos dar aquela recapitulada nas equações de energia.
O trabalho realizado pela força gravitacional pode ser encontrado da seguinte forma:
Onde:
é a variação da energia térmica
é a variação da energia mecânica que pode ser separada em cinética e potencial, dessa forma.
Onde:
é a variação da energia cinética
é a variação da energia potencial, que podemos isolar pois é aí que a gente quer chegar.
Passo 2
Agora vamos calcular cada uma das energias que a gente precisa, beleza?
A variação de energia térmica pode ser encontrada través da equação:
Onde:
é a força de atrito
é a distância percorrida.
E o trabalho mecânico realizado pelo bloco pode ser dado por:
Onde:
é a força que age sobre o bloco.
Passo 3
Enfim, voltando a nossa equação da energia no passo 1, a qual isolamos a variação da energia gravitacional a gente vai substituir geral que foi encontrado.
Lembrando que a energia cinética nos foi dada e tem valor
Podemos substituir enfim.
Logo, o trabalho realizado pela força gravitacional é