Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Na Fig. 9-67, o bloco 1 de massa desliza sem velocidade inicial ao longo de uma rampa sem atrito a partir de uma altura e colide com o bloco 2 de massa , inicialmente em repouso. Após a colisão, o bloco 2 desliza em uma região onde o coeficiente de atrito cinético é e para depois de percorrer uma distância nessa região. Qual é o valor da distância se a colisão é (a) elástica e (b) perfeitamente inelástica?
Passo 1
A primeira coisa a se fazer é achar a velocidade do bloco quando ele atinge o solo, tranquilo?
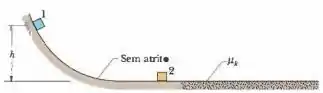
Pra isso, podemos usar a conservação da energia mecânica. Como no topo não há velocidade e no solo não há potencial gravitacional, podemos igualar:
Passo 2
Beleza galera, agora vamos considerar que a colisão é elástica.
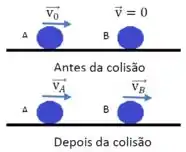
Pela conservação de momento linear, podemos relacionar as velocidades antes e imediatamente depois da colisão:
Como queremos na verdade a velocidade do bloco depois da colisão () e sabemos a velocidade do bloco antes da colisão (), podemos pegar essas duas equações e substituir com o que sabemos:
E logo, substituindo na primeira equação desse passo, temos:
Agora, pela conservação da energia cinética, temos:
Daqui em diante a gente vai manipular a beça as fórmulas, porque a conservação da energia cinética que vai nos salvar. Como todo mundo ta sendo dividido por , podemos tirar o denominador:
E substituir os valores conhecidos de e :
LÁÁÁ da conservação do momento linear, podemos substituir e num próximo passo cortar os . Saca só como fica:
Cortando o termo dos dois lados:
Lembrando que da conservação do momento linear, obtemos:
Substituindo obtido nessa última equação, ó só o que a gente encontra:
E tai a velocidade do corpo que passará pela região com atrito no caso da colisão elástica!
Passo 3
Para uma colisão perfeitamente inelástica:
Pela conservação de momento linear, podemos relacionar as velocidades antes e imediatamente depois da colisão:
Usando nossas considerações do passo :
E tai a velocidade do corpo que passará pela região com atrito no caso da colisão perfeitamente inelástica!
Passo 4
Show galera, resumindo os dois últimos passos, achamos que o corpo que passará pela região com atrito é, em cada caso:
Usando o teorema de que a variação da energia mecânica é igual ao trabalho das forças não conservativas, achamos:
Como a velocidade final é zero porque chega no repouso:
Como a normal se iguala a força peso:
Para nossos casos então vamos ter:
Note que:
Portanto, substituindo os valores, achamos: