Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.Problemas Adicionais - Ex. 94

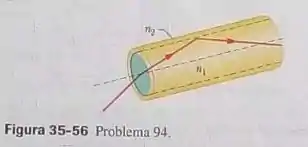
A Fig.35-56 mostra uma fibra ótica na qual um núcleo central de plástico, com um índice de refração n 1 = 1,58 , é envolvida por um revestimento de plástico com um índice de refração n 2 = 1,53 .   Os raios luminosos se propagam ao longo de diferentes trajetórias no núcleo central, o que leva a diferentes tempos de percurso, isso faz com que um pulso de luz inicialmente estreito de alarguração trafegar pela fibra o que reduz a qualidade do sinal. Considere a luz que se propaga ao longo do eixo central e a luz que é refletidamente com o ângulo crítico na interface entre o núcleo e o revestimento. Qual é a diferença entre os tempos de percurso para uma fibra ótica com 300m de comprimento.

Passo 1

Primeiramente quanto tempo leva para o raio luminoso que se propaga com velocidade c chegar até o final da fibra ótica:

t d i r e t o = L v 1 = n 1 L c

Passo 2

Para a fibra ótica o que importa é a velocidade paralela que importa. Se decompormos ela utilizando a Lei de Snell nós da v 1 s e n θ c = v 1 n 2 n 1 .

Logo o tempo que esse raio demora pra completar o percurso será:

t d i a g o n a l = L v 1 s e n θ c = n 1 2 L c n 2

Passo 3

A diferença de tempo será Δ t = t d i a g o n a l - t d i r e t o = n 1 2 L c n 2 - n 1 L c = n 1 L c n 1 n 2 - 1 =

= 1,58 300 3,0.10 8 1,58 1,53 - 1 = 51,6   n s

Resposta

51,6   n s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 33-71, dois raios luminosos que se estavam se propagando no ar passam por cinco placas de plástico transparente e voltam para o ar. As placas tem interfaces paralelas e espessura desconhecid
A Fig.35-57 mostra um jogo de fliperama que foi lançado no Texas. Quando pistolas de lasers são apontadas para o centro de um conjunto de placas de plástico, onde se encontra o alvo, um tatu de barro.
Na Fig. 35-33, um raio luminoso incide com um ângulo θ 1 = 50 ° em uma série de cinco placas transparentes com interfaces paralelas. Para as placas 1 e 3, L 1 = 20 μ m , L 3 = 25 μ m , n 1 = 1,6 e n 3
No modelo simplificado de fibra ótica discutido na Seç. 2.4 (cilindro circular de vidro), calcule o ângulo de incidência θ máximo na face de entrada (fig.) para o qual a luz será guiada dentro da fibr