Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 15.Exercícios e Problemas - Ex. 43

A Figura 15.19 mostra um elevador hidráulico com uma força F → 1 equilibrando outra força F → 2 Suponha que a força F → 2 seja o peso invariável m g de um objeto de massa m . Derive a Equação 15.13, a qual significa que o incremento de força necessário para erguer o peso em uma distância d 2 é ∆ F = ρ g A 1 + A 2 d 2 , onde ρ é a densidade do líquido

Passo 1

Bom! Vamos começar fazendo um esboço do nosso problema, pra ajudar a gente a entender melhor o que tem que fazer...

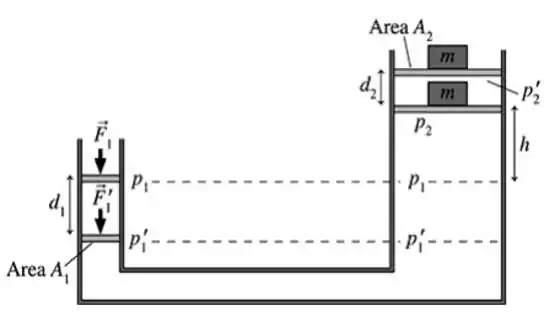
Pela figura, aplicando o Teorema de Stevin, podemos ver que...

p 1 = p 2 + ρ g h

Quando F 1 é aumentado para F 1 ' , o peso é elevado a uma distância de d 2 e o pistão esquerdo é abaixado através de uma distância d 1 . As pressões p 2 ' e p 1 ' estão agora relacionadas através do Teorema de Stevin, por...

p 1 ' = p 2 ' + ρ g ( h + d 1 + d 2 )

Subtraindo essa segunda equação da primeira...

p 1 ' - p 1 = p 2 ' + ρ g h + d 1 + d 2 - p 2 - ρ g h

p 1 ' - p 1 = p 2 ' - p 2 + ρ g d 1 + d 2

Passo 2

Sabemos que...

p 1 = F 1 A 1

p 1 ' = F 1 ' A 1

E também...

p 2 ' = m g A 2

Pelo que a equação do final do P a s s o   1 vai ficar assim...

p 1 ' - p 1 = p 2 ' - p 2 + ρ g d 1 + d 2

F 1 ' A 1 - F 1 A 1 = m g A 2 - m g A 2 + ρ g d 1 + d 2

F 1 ' - F 1 A 1 = ρ g d 1 + d 2

F 1 ' - F 1 = ρ g A 1 d 1 + d 2

∆ F = ρ g A 1 d 1 + d 2

∆ F = ρ g A 1 d 1 + A 1 d 2

Uma vez que o óleo é incompressível, pelo teorema de Pascal temos que...

A 1 d 1 = A 2 d 2

Assim, substituindo isso na fórmula do ∆ F :

∆ F = ρ g A 1 d 1 + A 1 d 2

∆ F = ρ g A 2 d 2 + A 1 d 2

∆ F = ρ g A 2 + A 1 d 2

Obtemos exatamente a relação do enunciado!

Resposta

∆ F = ρ g A 2 + A 1 d 2

Ver Outros Exercícios desse livro