Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 78
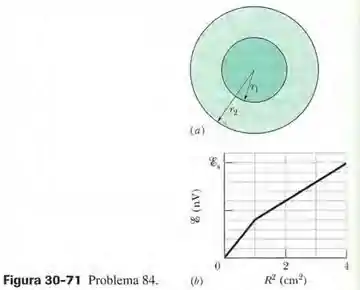
A figura 30-71a mostra duas regiões circulares concêntricas nas quais campos campos magnéticos uniformes podem variar. A região q, com um raio , possui um campo magnético dirigido para fora do papel cujo módulo está aumentando. A região 2, com uma raio , possui um campo magnético dirigido para fora do papel que também pode estar variando. Um anel condutor de raio , concêntrico com as duas regiões, é instalado e a força eletromotriz em função do quadrado do raio do anel, para . A escala do eixo vertical é definida por . Determine os valores das taxas (a) e (b) . (c) O módulo de está aumentando, diminuindo ou permanece constante?
Passo 1
Bom, galera, o módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Se a gente considerar apenas uma espira, uma área constante e uma campo variável no tempo, temos:
O que significa que a inclinação das retas da figura 30-71b é igual a .
Como a inclinação da reta da esquerda é , temos:
Passo 2
Como a inclinação da reta da direita , temos:
De acordo com a lei de Lenz, o módulo de está aumentando.
Resposta
- ;
- ;
- De acordo com a lei de Lenz, o módulo de está aumentando.