Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 49
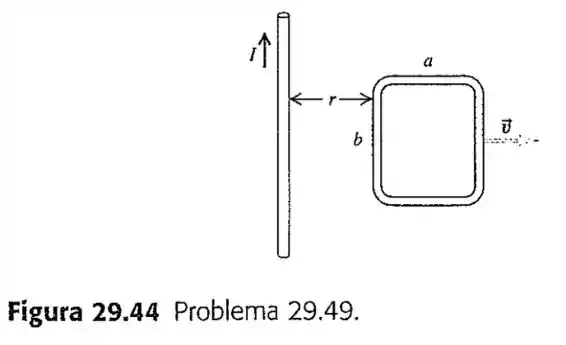
49- Na Figura , a espira está sendo puxada para a direita a uma velocidade escalar constante . Uma corrente constante flui pelo fio longo, no sentido indicado.
Calcule o módulo da fem induzida resultante na espira. Faça isso de duas formas: usando a lei de Faraday da indução (Sugestão: veja o Problema ) e analisando a fem induzida em cada segmento da espira em função do seu movimento
Determine o sentido (horário e anti-horário) da corrente induzida na espira. Faça isso de duas formas: usando a lei de Lenz e usando a força magnética sobre as cargas na espira.
Confira sua resposta para a fem no item nos seguintes casos especiais, para verificar se é razoável em termos físicos: a espira está estática; a espira é muito delgada, portanto ; a espira fica muito distante do fio
Passo 1
Uma questão de três letras mas com várias formas de resolver ela, dá um pouco de preguiça né? Mas agarra na minha mão e vamos fazer ela com paciência.
Utilizando a lei de Faraday, nós teremos primeiramente que saber o fluxo magnético nessa espira, e que será causado pelo fio longo e valerá:
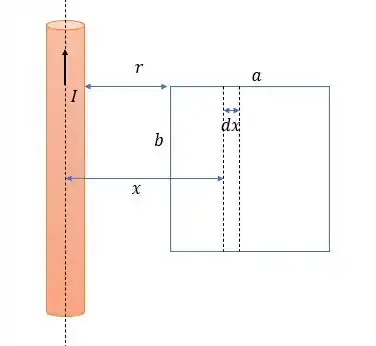
O que dá:
Então como a corrente é constante, na real tudo nessa fórmula aí é constante, menos a posição dessa espira, portanto devemos fazer o seguinte:
Não esqueça da regra da cadeia!
Portanto a fem que é calculado por será:
Isso responde a da letra .
Passo 2
Para fazer a da letra nós devemos ter noção que a tensão fem causada pela fórmula só é causada quando a barra e a velocidade são perpendiculares, ou seja as duas barras horizontais não geram nenhuma tensão induzida.
Além disso precisamos saber que a corrente nessa espira flui numa direção somente, então a diferença de tensão será causada da barra mais próxima do fio (que tem mais campo magnético, portanto tem um maior campo elétrico) reduzido da barra mais distante (menos campo, portanto menos campo elétrico) a diferença entre tensões entre elas nos dará a fem total na espira. Ou seja:
Então:
Passo 3
Agora vamos ver o sentido da corrente na espira pela lei de Lenz e para isso nós precisamos ver duas coisas, a corrente (pela regra da mão direita) gera um campo magnético que entra no centro da espira, e quando deslocamos a espira para a direita esse campo magnético tende a diminuir e a Lei de Lenz nos diz que a espira tende a manter a direção dessa espira, portanto o campo magnético induzido será de entrar no centro da espira também e essa corrente estará no sentido horário.
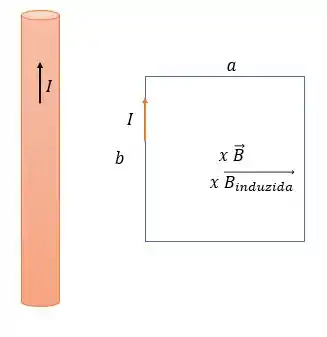
Passo 4
Agora resolvendo a na letra , vemos que pela regra da mão direita o campo magnético na espira entra na folha do papel e como a velocidade aponta para a direita e a corrente aponta na direção da força magnética (para cargas positivas) então a força na magnética na carga positiva aponta na mesma direção da carga do fio da fonte (olhando pro fio da espira mais próximo a fonte de campo magnético) . Portanto a corrente é no sentido horário.
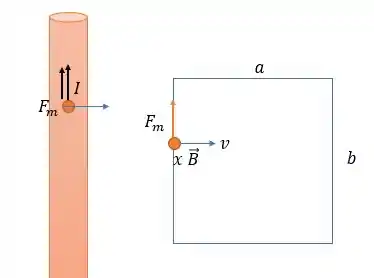
Passo 5
Resolvendo a letra , número
Quando a espira está estática e quando , pois veja o lance da velocidade alterar na fem é por que ela altera no campo magnético que atua sobre a espira, então como nem a área e nem o campo magnético variam então realmente não haverá fem na espira.
Numero
Quando temos:
Quando tende a zero as duas barras verticais ficam juntas, então surge um potencial elétrico mas que não tem para onde correr, portanto não flui corrente.
Numero
Quando a espira é muito distante do fio , e o campo magnético tende a ser nulo, portanto: