Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 35.Exercícios e Problemas - Ex. 40

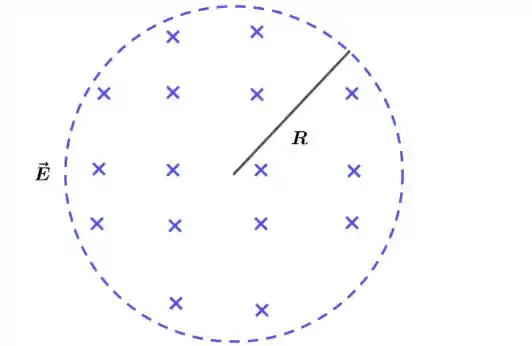
A FIGURA 35.40 representa o campo elétrico no interior de um cilindro de raio R = 3,0 mm. A intensidade do campo aumenta com o tempo de acordo com a função E   =   1,0 ∙ 10 ⁸   t ²   V / m , onde t está em s. O campo elétrico fora do cilindro é sempre nulo, e dentro o campo era nulo para t

a. Obtenha uma expressão para o fluxo elétrico e através do cilindro inteiro em função do tempo.

b. Desenhe uma figura que mostre as linhas do campo magnético no interior e no exterior do cilindro. Inclua pontas de setas no desenho para indicar a orientação do campo.

c. Obtenha uma expressão para a intensidade do campo magnético em função do tempo a uma distância r R do centro. Calcule a intensidade do campo magnético para r

d. Obtenha uma expressão para a intensidade do campo magnético em função do tempo a uma distância r R do centro. Calcule a intensidade do campo magnético para r

Passo 1

  1. Temos que encontrar uma expressão para o fluxo elétrico Φe​ através de todo o cilindro em função do tempo.

    2. A área do cilindro é dada por A= π R². Assim, o fluxo elétrico através do cilindro em função do tempo é dado por:

    Φ E ( t )   =   A ∙ E ( t )   =   π R ² ( 1 ∙ 10 ⁸ ) t ²   V / m

    Passo 2

  2. Temos que fazer um desenho. As linhas do campo magnético estão orientadas em círculos no sentido horário dentro e fora do cilindro.

  3. Devemos encontrar uma expressão para a intensidade do campo magnético em função do tempo a uma distância r

    Da lei de Ampere-Maxwell em um círculo de raio r

    ∮ B _ ∙ d _ s   =   1 c ² d Φ e n c d t

    Do anterior, temos que encontrar valor para B:

    ∮ B _ ∙ d _ s   =   1 c ² d Φ e n c d t

    B ( r ) 2 π r   =   1 c ² π r ² d E d t   =   1 c ² π r ² ( 10 ⁸ ) ( 2 t )   V / m

    B ( r )   =   10 ⁸ c ² t r   V / m r   =   2.0   m m   /   t   =   2 s

    B   =   4.4 ∙ 10 ⁻ ¹ ²   T

  4. d.) Temos que encontrar uma expressão para a intensidade do campo magnético em função do tempo a uma distância r>R do centro.

Da lei de Ampere-Maxwell em um círculo de raio r>R , temos:

B ( r ) ∙ 2 π r   =   1 c ² π R ² d E d t   =   1 c ² π R ² ( 1.0 ∙ 10 ⁸ ) ( 2 t )   V / m

B ( r )   =   10 ⁸ c ² t R ² V/m onde r   =   4.0   m m   e   t   =   2 s

B   =   5 ∙ 10 ⁻ ²   T

Resposta

  1. Φ E ( t )   =   A ∙ E ( t )   =   π R ² ( 1 ∙ 10 ⁸ ) t ²   V / m
  2. b.) As linhas do campo magnético estão orientadas em círculos no sentido horário dentro e fora do cilindro.
  3. B   =   4.4 ∙ 10 ⁻ ¹ ²   T
  4. B   =   5.0 ∙ 10 ⁻ ¹ ²   T
Ver Outros Exercícios desse livro