A Figura G.1.10 mostra uma cabeça inclinada para a frente. A cabeça pesa e é suportada pela forca muscular exercida pelos músculos do pescoço, e pela força de contato , exercida na junta atlantooccipital. Dada a forca , , e a sua direção formando um angulo de com a horizontal, calcule à forca para manter a cabeça em equilíbrio.
Passo 1
Primeiramente vamos fazer o diagrama de corpo livre, para esquematizar todas as forças, e como elas atuam em seus respectivos pontos de ação:
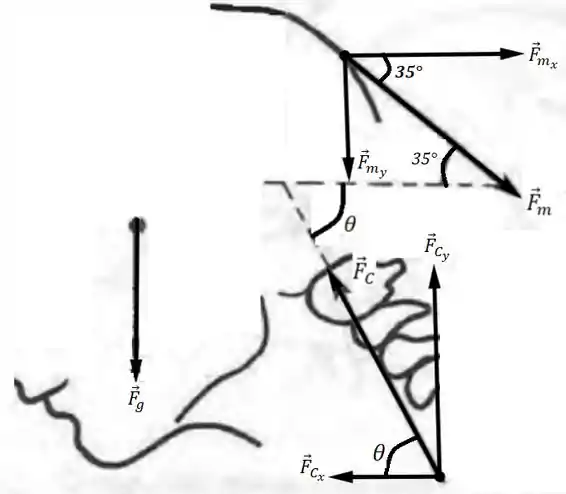
Com o DCL esquematizado, podemos analisar as forças atuantes, e então deduzir as condições de equilíbrio para a solução do problema:
Passo 2
O enunciado pede para manter a cabeça em equilíbrio:
Com isso podemos utilizar as equações de equilíbrio estático:
Passo 3
Vamos analisar as forças em :
Passo 4
Vamos colocar as forças em função das resultantes: :
Analisando as forças resultantes em seus respectivos pontos de ação, definimos que:
Subst. tudo em:
Passo 5
Vamos analisar agora, as forças em :
Passo 6
Semelhante o que fizemos em , vamos fazer em , colocar as forças em função das resultantes: usando as mesmas condições:
Subst. tudo em:
Passo 7
Como o valor de são fornecidos no enunciado, temos duas equações com duas incógnitas:
Primeiro passo a partir de agora, é ver se conseguimos através de alguma operação elementar, eliminar uma das duas incógnitas:
Se optarmos por dividir , eliminaremos e determinamos , pois , vamos efetuar a divisão:
Passo 8
Subst. os valores numéricos fornecidos pelo exercício temos , e :
Passo 9
Subst. em uma das equações , determinamos :
Usando a equação , temos:
Subst. os valores numéricos:
Resposta