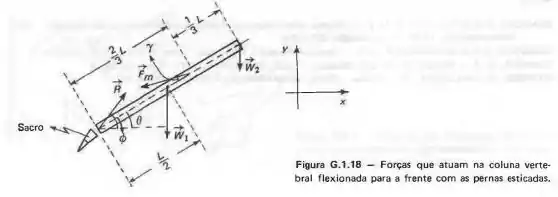
A Figura G.1.18 esquematiza as forças que atuam na coluna vertebral flexionada para a frente; a coluna é substituída por uma barra rígida de comprimento L. Esse esquema é válido para o movimento de flexão das costas com as pernas esticadas. O peso do tronco é ; é a som a dos pesos dos braços e da cabeça; é a força exercida pelos músculos eretores da espinha; e é a reação do sacro sobre a espinha.

Determine as intensidades de e em função do peso do indivíduo. Qual é o ângulo que faz com a horizontal? Qual é a força de compressão exercida pelo sacro sobre o disco lombossacral, ou seja, a componente de perpendicular ao sacro?

Suponha que , , e .

Para o sistema estar em equilíbrio, temos que satisfazer duas condições. A primeira é

Se somarmos todas as forças que estão em e em temos que ter o valor zero. E a segunda é

Se somarmos todos os torques, vamos ter o valor zero também. Vamos começar pelas forças em x.

Se olharmos a figura, as únicas forças que tem componentes na direção são e . Vamos ter então

Para termos o valor, temos que observar a imagem e ver o ângulo que o vetor faz com a horizontal e vertical, na direção onde está. No caso de vemos que o ângulo que ele faz com a direção da coluna é . Então temos que decompor esse ângulo para descobrir e de forma que

E

Para o temos a mesma coisa, com o detalhe que o ângulo que nos foi dado é o ângulo com relação a barra. Temos que usar o ângulo que essa força faz com a horizontal. Como o ângulo todo tem o mesmo ângulo que a inclinação da barra com a horizontal, vamos ter que

Assim

Como temos os valores desses ângulos, podemos facilmente achar o valor de sigma e o usando pra achar as componentes de temos

E

Agora vamos considerar cada direção e ver o que podemos descobrir.

Na direção temos

Isolando temos

Na direção , vamos ter

Substituindo o valor de que obtemos

Agora só precisamos achar o ângulo para termos os valores. Para isso, aplicamos a segunda condição.

Para a segunda condição, precisamos ter primeiro um ponto onde vamos considerar que é o ponto de apoio, que pode ser qualquer um dos pontos que temos. Vou considerar que é esse ponto de apoio. Vamos ter que decompor as forças para termos as componentes perpendiculares a barra. Então

Agora calculando o torque em relação a temos

Substituindo os valores, temos

Substituindo o valor para achar o valor do ângulo, temos

Isolando temos

Substituindo os valores temos

E por fim substituindo os valores para achar o valor de temos

E para a direção perpendicular temos