A Figura G.1.9 esquematiza o joelho. A tensão T → é exercida pelo tendão quadríceps quando passa pela rótula. Supondo que T → seja 160 N , determine a força de contato F → C exercida pelo fêmur sobre a rotula.

Enunciado

Primeiramente vamos fazer o diagrama de corpo livre, para esquematizar todas as forças, e como elas atuam em todos os pontos:

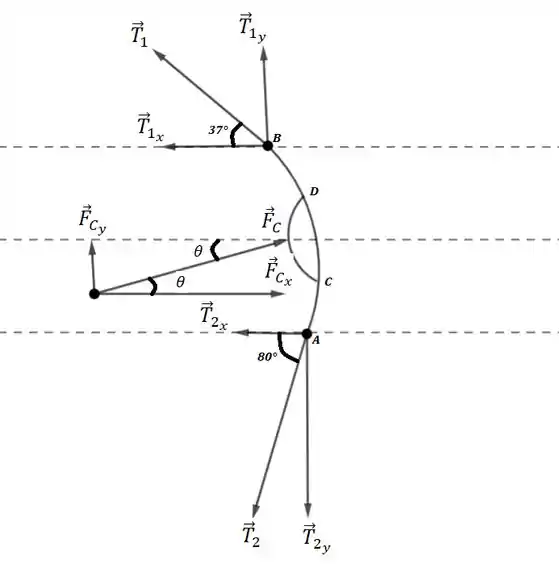
Com o DCL esquematizado, podemos analisar as forças atuantes, e então deduzir as condições para as possíveis solução do problema:

Considere o arco como o tendão quadríceps, e o arco como a rótula do joelho.

Vamos considerar o joelho como um sistema em equilíbrio:

Com isso podemos utilizar as equações de equilíbrio estático:

Vamos analisar as forças em :

Vamos colocar as forças em função das resultantes: :

Como o tendão é o mesmo em toda a extensão, é como se fosse um fio ideal em uma polia, com isso sabemos que: :

Subst. tudo em:

Vamos analisar agora, as forças em :

Semelhante o que fizemos em , vamos fazer em , colocar as forças em função das resultantes: , usando as mesmas condições:

Subst. tudo em:

Voltando para a expressão acima, nossa equação de equilíbrio em , fica assim:

Como o valor de é fornecido no enunciado, temos duas equações com duas incógnitas:

Primeiro passo a partir de agora, é ver se conseguimos através de alguma operação elementar, eliminar uma das duas incógnitas:

Se optarmos por dividir , eliminaremos e determinamos , pois , vamos efetuar a divisão:

colocando em evidência no lado direito, simplificamos a equação ainda mais:

Subst. em uma das equações , determinamos :

lembrando que

Usando a equação , temos:

Subst. os valores numéricos: