Determine as intensidades das forças abdutora , e de contato, , assim como a direção de em relação a vertical. Considere o peso da perna direita do peso total e que a perna esquerda não está apoiada. De sua resposta em função do peso total .
Como a pessoa está parada, a perna pode ser substituída por uma barra rígida. Escolha de modo conveniente o ponto em relação.
Passo 1
Abaixo está o DCL, com todos as forças esquematizadas, nos seus respectivos pontos de ação:
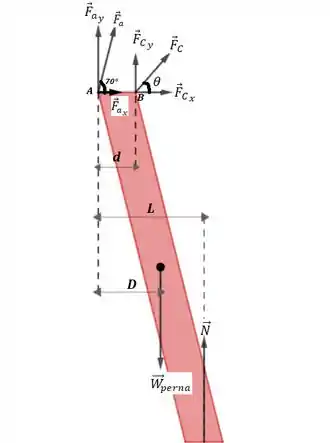
Considere a barra vermelha como a perna:
Força abdutora
Força de contato
= Peso da perna
= Forca normal (contato com o chão)
= Peso da pessoa
Passo 2
Como o corpo está parado, com isso vale as equações de equilíbrio estático.
Vamos deduzir nossas equações de equilíbrio, usando analisando o DCL:
Passo 3
Vamos para as forças em :
Sabemos que e são componente horizontal de :
Subst. em:
Passo 4
Em temos:
Semelhante o que fizemos em faremos em , pois e são componente vertical de :
Outra informação que sabemos é que , e que :
Portanto o lado direito da equação , é dado por:
subst. tudo em :
Passo 5
Vamos calcular o torque no ponto , adotando sentido anti-horário como positivo:
Como sabemos que, , subst. tudo temos:
Tirando em evidência, temos:
Subst. os valores de , fornecidos no enunciado:
Subst. :
Passo 6
![]()
Subst. em 2 temos
![]()
Dividindo os dois lados por 118, temos:
fazendo o inverso dos dois lados temos:
Como , subst. temos:
Resposta