Na figura, qual é o menor valor do módulo da força horizontal constante aplicada horizontalmente ao eixo da roda que permite à roda ultrapassar um degrau de altura ? O raio da roda é e a massa é .

Passo 1
Primeiro, vamos identificar as forças atuantes, como representamos nesta figura:
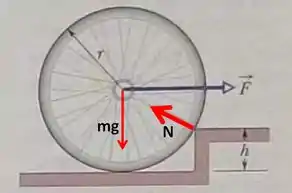
Passo 2
Outro passo importante é relacionar o ângulo que determina a direção de com aquele formado pela linha central e a horizontal, assim como na figura:

Temos todos os ingredientes agora para encontrarmos o valor de pedido na questão! Ela nos pede o menor valor de para que a roda consiga girar sobre o degrau. Isso só vai acontecer se o torque total exercido por essas forças (no sentido do vetor que entra no plano do papel) não for nulo , pois nesse caso a roda não está parada, em equilíbrio, mas está girando quando consegue ultrapassar o degrau.
Passo 3
Considerando a situação limite em que a roda consegue fazer a ultrapassagem, temos:
Passo 4
Vamos agora encontrar o valor de Com ele, conseguimos isolar na equação acima e encontrar a resposta. Para isso, vamos voltar a analisar a figura do passo 2:
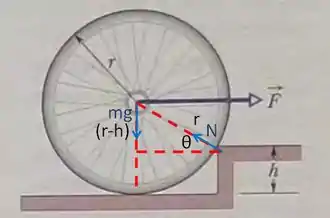
Nela, note que
Passo 5
Pronto! Agora é só “jogar” o valor do acima na equação do passo 1:
Substituindo os valores do enunciado,temos: