Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.2 - Ex. 18
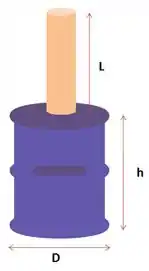
Na Figura, um tubo aberto, de comprimento e área de seção transversal , está fixado no topo de um barril cilíndrico de diâmetro e altura. O barril e o tubo são cheios d’água (até o topo do tubo). Calcule a razão entre a força hidrostática sobre o fundo do barril e a força gravitacional sobre a água contida no barril. Por que esta razão não é igual a ?
Passo 1
Show de bolinhas galerinha bonita, nesse exercício aqui o enunciado nos deu um um tubo aberto conectado a um barril como na figura abaixo:
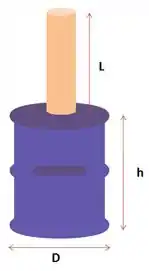
Sabendo que o tubo e o barril estão cheios de água até o topo, com o tubo aberto tendo um comprimento e área de seção transversal , e o barril cilíndrico de diâmetro e altura, o enunciado pede pra gente encontrar a razão entre as forças hidrostática no fundo do barril e a força gravitacional SOBRE a água do barril.
Iradoso, pra isso primeiro vamos lembrar que a pressão hidrostática é dada como:
Onde é a área onde é exercida a pressão, ok? Vamos continuar.
No fundo do barril, temos uma força devido à pressão hidrostática exercida por toda a água no tubo e no barril sobre o fundo do barril. Então:
Onde é a força no fundo do barril, é a pressão no fundo do barril e é a área do fundo do barril.
Já sobre a água do barril, temos que a força peso da água no interior do barril é:
Só que , logo . Então:
Onde é a força no topo do barril, é a densidade da água, é a aceleração da gravidade e é o volume de água no barril. O volume pode ser calculado por área da base vezes a altura:
Já que é um barril cilíndrico. Então:
E a razão entre as duas é:
Podemos cortar as áreas, pois são iguais logo:
Só que é justamente a pressão hidrostática no fundo do barril!!
Então, temos que saber a razão entre as pressões no topo e no fundo do barril! Bora lá!
Passo 2
Belezoca, aqui a gente precisa lembrar que a pressão hidrostática é aquela que ocorre no interior dos líquidos, sendo exercida pelo peso do próprio líquido. Logo, considerando uma coluna de líquido de altura , vamos obter que:
Só que a densidade é dada como:
Enquanto que o volume que o líquido ocupa depende do recipiente, logo para calcular o volume de líquido, usamos área da base vezes a altura:
Ou seja:
Substituindo essa massa na pressão hidrostática:
Passo 3
Assim, como a altura no fundo do barril () é o dobro da altura no fundo do tubo (), substituindo na equação do passo 1:
Substituindo:
A diferença entre essas pressões deve-se à força adicional exercida pela presença da água no tubo. E isso que impede que a razões entre elas seja unitária.