Enunciado
Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 15.Exercícios e Problemas - Ex. 34
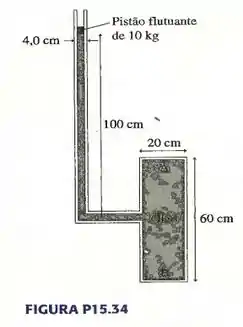
a. Na FIGURA P15.34, quanta força o fluido exerce sobre a extremidade A do cilindro?
b. Quanta força o fluido exerce sobre a extremidade B do cilindro?
Passo 1
a) Nesse primeiro item aqui, temos que achar a força que o fluido exerce sobre a extremidade do cilindro!
Pois muito bem! Lembra lá qual a fórmula da pressão agindo sobre uma superfície?
Pois muito bem! Ela é dada por...
Agora presta atenção! O cilindro tem massa e está em contato com a atmosfera!
Isso quer dizer que a pressão a que o sistema está submetido lá no começo onde fica o pistão é dada por...
Que é a soma da pressão atmosférica com o peso do pistão agindo sobre uma seção transversal de !
Calculando :
Passo 2
Continuando nosso raciocínio, pra achar a pressão agindo sobre o cilindro, temos que usar o Teorema de Stevin...
Sabendo , a pressão abaixo (que é onde está o ponto ), será dada por...
Como a densidade do óleo é de :
E uma vez descoberta a pressão agindo sobre o cilindro, pra achar a força que o fluido exerce basta multiplicar essa pressão pela área da seção transversal do cilindro, que é um círculo de raio ...
Passo 3
b) Pra esse segundo item aqui, é o mesmo procedimento!
A diferença é que vai estar abaixo. Logo;
E então, calculando a força exercida...
Resposta
a)
b)