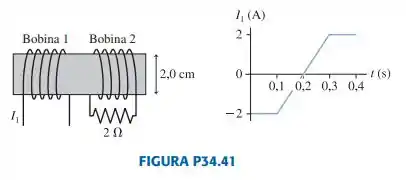
A FIGURA P34.41 representa duas bobinas com 20 espiras cada uma, feitas de um fio com diâmetro de firmemente enrolado sobre um mesmo cilindro comprido com diâmetro de . A corrente através da bobina 1 é representada no gráfico. Determine a corrente na bobina 2 nos instantes (a) s e (b) t 0,25 s. Uma corrente é considerada positiva se ela entra na página na parte superior das espiras. Considere que o campo magnético da bobina 1 passe inteiramente através da bobina 2.
Passo 1
Faaaaaala, galera... Tranquileba??
Assumiremos que o campo magnético da bobina 1 passa através da bobina 2 e que podemos usar o campo magnético de um solenoide pra bobina 1.
Assim:
Sabemos que:
Sendo B constante em todo o caminho, e para um solenoide:
Sendo:
Logo:
De modo que:
Bora pro próximo passo?!
Passo 2
Para a)
Veja que de a corrente é constate, logo
Passo 3
Veja que a corrente entre a corrente é
Assim:
Concluímos que:
Resposta
a)
b)