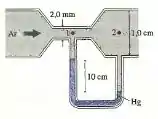
O ar flui pelo tubo mostrado na FIGURA P15.65. Suponha que o ar comporte-se como um fluido ideal.
a. Quanto valem as velocidades e nos pontos 1 e 2?
b. Qual é a vazão de volume correspondente?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Agora o problema as velocidades, que vai seguir praticamente o mesmo processo do que para encontrar a altura, obviamente, vai aparecer a raíz, visto que na fórmula de Bernoulli, os termos de velocidades aparecem elevados ao quadrado.
Com isso, segue o fio, com o mesmo processo, a variação de é dada por
Para a equação de continuidade nos sabemos que
Isolando o , temos que
Agora é substituir a área A pela a área do círculo, que dará algo mais ou menos assim
Passo 2
Agora já podemos escrever a fórmula para a diferença de pressão, já que temos as relações entre as velocidades
A diferença de pressão é dada pela altura da coluna de mercúrio, desse jeito aqui
Com isso, temos que
Agora, vamos isolar o (por isso que falei que teria uma raíz)
Agora é somente substituir os valores numéricos
O termo será, portanto,
Passo 3
B – A taxa envolvendo o fluxo pode ser calculada sabendo que , com isso nós obtemos
Substituindo os valores, nós temos
Logo, a taxa Q é igual a