Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 70

Um foguete de 25000 kg é lançado verticalmente da superfície terrestre com velocidade constante. Durante o movimento considerado neste problema, suponha que g permanece constante (ver Capítulo 12). No interior do foguete, um instrumento de 15,0 N está suspenso por um fio capaz de suportar uma tensão de 35,0 N. a) Ache o tempo mínimo necessário para o foguete atingir a barreira do som (330 m/s) sem romper o cabo no seu interior e a força propulsora vertical máxima dos motores do foguete sob essas condições. b) A que distância acima da superfície terrestre está o foguete, quando rompe a barreira do som?

Passo 1

Aqui, nós vamos aplicar a segunda equação de Newton ao objeto de aceleração, e para calcular a aceleração utilizando as equações de aceleração constante para descrever o movimento.

Vamos, então, esboçar o diagrama de corpo livre para esse objeto.

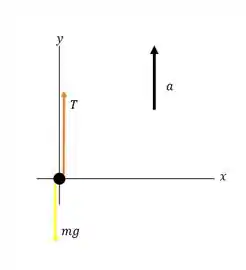
Este possui massa m = P g = 1.531 k g

Passo 2

  1. Podemos observar que só temos forças na vertical, então, vamos aplicar a segunda lei de Newton no e i x o   y :

    2. ∑ F y = m a y

    T - m g = m a

    ⇒ a = T - m g m

    Temos que: T = 35 N m = 15 g   k g g = 9,8 m / s 2

    Então,

    a y = 35 N - 15 9,8 k g ⋅ 9,8 m / s 2 15 9,8 k g = 13,07 m / s 2

    Passo 3

    Também temos que: v 0 y = 0 v y = 330 m / s a y = 13,07 m / s 2

    Queremos encontrar o tempo, t , então vamos utilizar a equação:

    v y = v 0 y + a y t

    ⇒ t = v y - v 0 y a y

    t = 330 m / s - 0 13,07 m / s 2 = 25,3 s

    Passo 4

    Considerando as forças no foguete, tem a mesma aceleração a y .

    E então, seja F o impulso dos motores do foguete, aplicando a segunda lei de Newton, temos que:

    F - m g = m a

    E isso implica que:

    F = m ( g + a )

    F = 25000 k g ⋅ ( 9,8 m / s 2 + 13,07 m / s 2 ) = 5,72 × 10 5 N

    Passo 5

  2. E para encontrarmos a que distância acima da superfície terrestre está o foguete utilizamos a equação:

∆ y = v 0 y t + a y t 2 2

∆ y = 0 + 13,07 m / s 2 ⋅ ( 25,3 s ) 2 2 = 4170 m

Resposta

  1. t = 25,3 s e F = 5,72 × 10 5 N
  2. ∆ y = 4170 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espaçonave decola verticalmente da Lua, onde g=1,6m / s ² . ² Se a nave tem uma aceleração vertical para cima de 1,0m / s ² ²no instante da decolagem, qual é o módulo da força exercida pela nave s
Um astronauta leva uma balança de banheiro para a Lua e fica em pé sobre ela. A balança marcará o peso dele? Explique.
Decida se cada uma das seguintes afirmações é verdadeira ou falsa. Em cada caso, explique sua resposta.a.A massa de um objeto depende de sua localização.b.O peso de um objeto depende de sua localizaçã
Suponha que você tente medir 100 g de sal usando uma balança de cozinha para realizar a medição dentro de um foguete que está subindo e acelerando. A quantidade de sal medida é muito maior, muito meno
As quatro bolas da FIGURA Q6.11 foram arremessadas diretamente para cima. Elas são de mesmo tamanho, mas possuem massas diferentes. A resistência do ar é desprezível. Ordene em sequência, do maior par