Uma força F que dura 20 s é aplicada a um corpo de massa igual a 500 kg. A força produz no corpo, que estava inicialmente em repouso, uma velocidade final de 0,5 m · s^-1. Se a força cresce linearmente com o tempo durante 15 se depois decresce até zero, também linearmente, durante 5 s, (a) determine o impulso causado sobre o corpo pela força, (b) calcule a força máxima exercida sobre o corpo, e (c) faça um gráfico de F contra l e procure a área sob essa curva. Esse resultado concorda com (a)? Suponha que F seja a única força que age no corpo.

Agora, na letra b, o exercício nos pede para encontrar a força máxima exercida pelo corpo. Vocês lembram as regrinhas da derivação aplicadas em aceleração? Vamos relembrar um pouquinho:

Quanto à velocidade, sabemos que ela é a derivada da equação horária do espaço, certo? Da mesma forma, quanto à aceleração, sabemos que ela é a derivada da equação horária da velocidade. Como queremos calcular uma força, precisaremos encontrar a aceleração. Assim, seguindo-se o que falamos até agora, temos:

, certo? Vamos dar uma ajeitada nessa equação:

Agora, vamos aplicar integral nos dois lados da equação! Uma observação importante: o tempo da velocidade varia de 0 a 0,5s e o da aceleração, de 0 a 20s. Então, temos:

Então, resolvendo a integração:

Além disso, sabemos que:

, logo, sabemos que

Agora, vamos substituir k e k’ na equação da aceleração encontrada acima:

Assim, como sabemos que, pela Lei de Newton, a força é dada por:

F=m*a, então, a força máxima será:

Logo, a força máxima é de 25N.

A letra c do exercício nos pede um gráfico de F contra t. Assim, lembrando que o tempo varia de 0 a 20 e a força cresce até 15s e passa a diminuir de 15 a 20s, então temos:

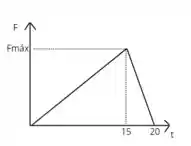
Para entender se o impulso deste gráfico é condizente com o que encontramos em a, vamos calcular a área do triângulo formado no gráfico, de base 20 e altura 25. Como a área do triângulo é dada por

,temos: