Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 2.Problemas - Ex. 16

Fótons de comprimento de onda 0,024 Å incide sobre elétrons livres. (a) ache comprimento de onda que é espalhado de um ângulo de 30° em relação a direção de incidência e energia cinética transmitida ao elétron. (b) faça o mesmo para um ângulo de espalhamento de 150°. (Sugestão: veja o exemplo 2-4)

Passo 1

Letra a

Informações do problema: comprimento de onda do fóton incidente 0,024 Å

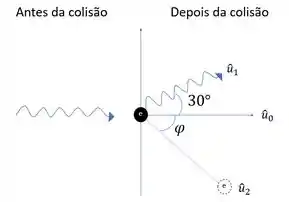Para o ângulo de 30° temos a ilustração abaixo:

Como no exemplo 2.4, o deslocamento Compton, é representado pela diferença entre os comprimentos de onda (espalhada e incidente).

Δ λ = λ ' - λ

E pode ser expresso também pela equação

Δ λ =   h m 0 c ( 1 - c o s θ )

Então, para determinar o comprimento de onda do fóton espalhado, temos que encontrar o deslocamento Compton. Sendo θ o ângulo entre a direção de incidência e a direção do espalhamento, temos θ = 30 ° nesse caso.

Δ λ =   h m 0 c ( 1 - 0,87 ) = 6,63   x   10 - 34 ( 9,11   x     10 - 31 )   ( 2,99   x   10 8 ) ( 1 - 0,87 )  

Δ λ = 0,32   x   10 - 12 m =   0,0032   Å

Então o comprimento de onda do fóton espalhado será dado por (não esqueça de conferir as unidades):

λ ' =   Δ λ + λ =   0,0032 + 0,024 =   0,027   Å

Passo 2

Como há conservação de energia, temos que:

E i - f o t . + m 0 c 2 = E f - f o t . + E f - e

E i - f o t . + m 0 c 2 = E f - f o t . + ( m 0 c 2 + K )

E i - f o t . = E f - f o t . + K

K =   E i - f o t . -   E f - f o t . =   - Δ E

Como descrito no exemplo 2.4, a energia do elétron depois da colisão, será a energia que o fóton incidente transfere para ele. Então para encontrar a energia de espalhamento do elétron, temos que saber a variação de energia do fóton.

Δ E =   E f -   f o t . - E i - f o t .

Sendo E =   h υ , então:

  E i -   f o t . =   h υ =   h c λ           e         E f -   f o t . =   h υ ' =   h c λ '

Logo:

Δ E =   h c λ -   h c λ ' =   h c   1 λ - 1 λ '

Δ E =   h c   1 λ - 1 λ ' =   ( 6,63   x   10 - 34 )   ( 2,99   x   10 8 ) 1 0,024   x   10 - 10 - 1 0,027   x   10 - 10

Δ E = 19,824 x 10 - 26 1 10 - 10 41,67 - 37,04

Δ E = 19,824   x   10 - 16   ( 4,63 ) =   91,78   x   10 - 16 J

Agora vamos transformar J → M e V

Δ E = 0,057   M e V

Passo 3

Letra B

Segue o mesmo raciocínio, porém o ângulo de espalhamento é diferente. Sendo θ o ângulo entre a direção de incidência e a direção do espalhamento, temos θ = 150 ° nesse caso.

Δ λ =   h m 0 c ( 1 - 0,87 ) = 6,63   x   10 - 34 ( 9,11   x     10 - 31 )   ( 2,99   x   10 8 ) ( 1 - ( - 0,87 ) )  

Δ λ = 0,45   x   10 - 12 m =   0,0045   Å

Então o comprimento de onda do fóton espalhado será dado por (não esqueça de conferir as unidades):

λ ' =   Δ λ + λ =   0,0045 + 0,024 =   0,028   Å

Passo 4

Analogamente, temos:

Δ E =   h c   1 λ - 1 λ ' =   ( 6,63   x   10 - 34 )   ( 2,99   x   10 8 ) 1 0,024   x   10 - 10 - 1 0,028   x   10 - 10

Δ E =     ( 6,63   x   10 - 34 )   ( 2,99   x   10 8 ) 41,67   x   10 10 -   35,71   x   10 10

Δ E =     ( 19,82   x   10 - 26 )   5,96   x   10 10

Δ E =     118,13   x   10 - 16   J

Agora vamos transformar J → M e V

Δ E = 0,074   M e V

Resposta

Para um ângulo de 30° temos:

K =   0,057   M e V

Para um ângulo de 150° temos:

K =   0,074   M e V

Ver Outros Exercícios desse livro