Um fóton de energia inicial eV que se move no sendo positivo do eixo x incidente sobre um elétron livre em repouso. O fóton é espalhado de um ângulo de 90°, indo no sentido positivo do eixo y. Ache as componentes do momento do elétron.
Passo 1
Informações do problema: energia inicial do fóton eV; Espalhado a um ângulo de 90°.
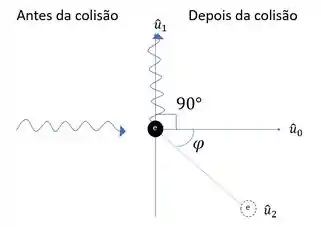
Vamos analisar a colisão- Conservação de momento:
Como podemos observar com a imagem ilustrativa da colisão, o momento após da colisão o momento do fóton e do elétron têm direções distintas:
Para encontrar as componentes do momento do elétron, é necessário fazer uma análise em cada eixo.
Passo 2
Analisando no eixo x (eixo horizontal), nesse eixo, a componente do momento final do fóton é nula, pois se encontra na direção .
Passo 3
Analisando no eixo y (eixo vertical), nesse eixo o momento inicial do é nulo, pois ele está na direção .
O sinal negativo do se deve ao fato de sua projeção está no sentido negativo do eixo. Sendo assim, temos:
Como não temos informações sobre a energia final do fóton, temos que escrevê-la em função da energia inicial do fóton.
Passo 4
Conhecemos a relação entre e , dada pelo exemplo 2.4 do livro.
Então, temos a energia final do fóton:
O pode ser escrito em função da energia inicial do fóton, já que ele é o comprimento de onda do fóton incidente.
Substituindo na equação da :
Colocando o em evidência o denominador, resultamos na equação:
Somando as frações do denominador (dentro das regras matemáticas), temos:
Como
Resposta
Agora podemos expressar as componentes do momento do elétron, com informações conhecidas: