O funcionamento do motor a gasolina de seu carro pode ser tratado pelo modelo do ciclo Ono representado na FIGURA PD19.71 . Uma mistura de combustível e ar é borrifada para dentro do cilindro. no ponto 1 do diagrama, quando o pistão está à máxima distância possível da vela de ignição. A mistura, então, é comprimida enquanto o pistão se move em direção à vela durante uma rápida compressão adiabática. A vela de ignição gera a faísca, no ponto 2, liberando energia ténnica armazenada na gasolina. O combustível queima tão rapidamente que o pistão não tem tempo de se mover, de modo que o aquecimento resultante é um processo isocórico. O gás quente e em alta pressão empurra, então, o pistão para fora, durame o c:urso de expansão. Finalmente, uma válvula de exaustão se abre, pennitindo que a temperatura e a pressão do gás caiam até seus valores iniciais antes de reiniciar o ciclo. a. Analise o ciclo Otto e demonstre que o trabalho reali1.ado a cada ciclo é dado por nR Wsai
Passo 1
E aiii gente, tudo bom com vocês?
Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!
Vamo lá!
Letra a:
Para o processo adiabático e:
Para o processo isocórico . Para o processo adiabático e
Para o processo isocórico . O trabalho feito por ciclo é:
Passo 2
Letra b:
A eficiência térmica do motor térmico é:
A última etapa decorre do fato de que . Vamos agora simplificar ainda mais esta expressão:
Da mesma forma, . A equação para eficiência térmica agora se torna:
Passo 3
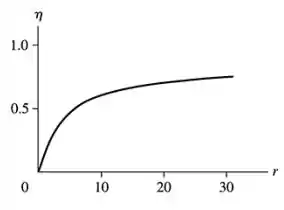
Resposta
- Ver gráfico