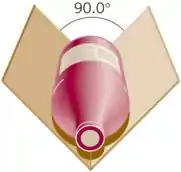
Uma garrafa de vinho vintage de 1,40 kg está deitada horizontalmente em uma prateleira, conforme mostrado no desenho. As duas superfícies nas quais a garrafa repousa, os apoios estão separados por , e a superfície direita faz um ângulo de 45,0 em relação à horizontal. Cada superfície exerce uma força na garrafa que é perpendicular à superfície. Ambas as forças têm a mesma magnitude F. Encontre o valor de F.

A soma dos ângulos dos apoios, dos dois lados, com a horizontal deve ser . Portanto, o ângulo que a superfície esquerda faz em relação à horizontal é

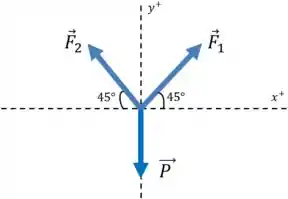
No diagrama de corpo livre da garrafa de vinho, o eixo é o horizontal. A força que cada superfície exerce sobre a garrafa é perpendicular às superfícies, então ambas as forças são direcionadas a acima da horizontal.

Deixando a superfície à direita ser a superfície 1, e a superfície à esquerda a 2, as forças e são mostradas no diagrama de corpo livre.

A terceira força que atua sobre a garrafa é , seu peso ou a força gravitacional exercida sobre ela pela Terra.

Vamos aplicar segunda lei de Newton e analisar as forças verticais neste diagrama de corpo livre para determinar a magnitude das forças e , usando o fato de que a garrafa está em equilíbrio.

As componentes verticais da força exercida pela superfície são

Mas as forças e tem a mesma magnitude , então temos as duas componentes verticais

Já que a garrafa está em equilíbrio, as forças no eixo devem ser equilibradas

Resolvendo a equação obtida para , temos: