Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 4.Problemas - Ex. 54
A viga de aço em formato de no desenho tem um peso de 8,00 kN e está sendo levantado a uma velocidade constante. Qual é a tensão em cada cabo preso às suas extremidades?
Passo 1
Opaaa tudo certo?
Vamos lá resolver mais uma questão muito interessante para nosso entendimento completo do capítulo!
A figura dada na questão é a seguinte:
Passo 2
O desenho mostrado abaixo assume que a direção positiva para cima, e mostra a viga junto com as três forças que agem sobre ele: seu peso e a tensão em cada um dos os cabos.
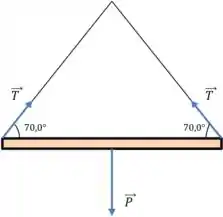
Uma vez que a viga está se movendo para cima em uma velocidade constante, sua aceleração é zero e está em equilíbrio.
Portanto, de acordo com a equação
a força líquida na direção vertical () deve ser zero, de modo que esta relação nos permitirá encontrar a magnitude da tensão.
Passo 3
O peso () é conhecido e o ângulo () também. Vamos considerar as componentes verticais e horizontais das forças. O que também é conhecido também, é que se move com uma velocidade constante, o que significa que a aceleração é zero.
Passo 4
A componente horizontal da tensão ()
Logo,
Passo 5
Fazendo o equilíbrio de forças na vertical, temos que:
Resolvendo para :