Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 49
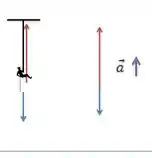
Uma ginasta de massa escala uma corda vertical que está presa no teto. Ignore o peso da corda. Desenhe um diagrama do corpo livre para a ginasta. Calcule a tensão na corda, considerando que a ginasta:
- Escala a uma taxa constante;
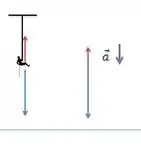
- Dependura-se estática na corda;
- Sobe a corda com aceleração de módulo ;
- Escorrega pela corda com aceleração de cima para baixo de módulo .
Passo 1
Se a ginasta escala a corda com velocidade constante (a taxa constante) isso significa que não há força resultante agindo sobre ela, então as únicas forças são a tração (em vermelho) e o peso (em azul) e elas devem se equilibrar:
Passo 2
Se a ginasta está estática, ou seja, em repouso, então as duas forças (tração e peso) também devem ser equilibradas, pois assim não há força resultante na ginasta:
Passo 3
Se ela sobe a corda com aceleração de módulo (representado em roxo), então temos que há força resultante e ela aponta para cima. Pela segunda lei temos:
Assim a tração (representada em vermelho) da corda é:
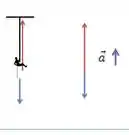O diagrama fica:
Passo 4
Se ela desce a corda com aceleração de módulo (representado em roxo) para baixo, então temos que há força resultante e ela aponta para baixo. Pela segunda lei temos:
Assim a tração (representada em vermelho) da corda é:
O diagrama fica:
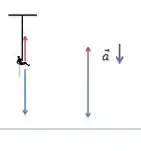
Resposta
