Para içar-se em uma árvore, um homem de 72,0 kg amarra uma das pontas de uma corda de náilon ao redor de sua cintura e joga a outra extremidade sobre um galho da árvore. Ele então puxa para baixo a extremidade livre da corda com uma força de 358 N. Despreze qualquer atrito entre a corda e o galho e determine a aceleração ascendente do homem.

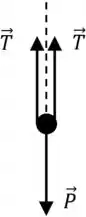
Para determinar a aceleração ascendente do homem por meio de Segunda lei de Newton, primeiro precisamos identificar todas as forças exercidas sobre ele e então construir um diagrama de corpo livre. Fiz um diagrama de corpo livre pra gente visualizar melhor o problema:

A Terra puxa para baixo o homem com força gravitacional . Assim que ele começar a acelerar para cima, ele não está mais em contato com o solo, então não há força agindo sobre ele.

A força de tração que ele exerce na corda faz não aparece em seu diagrama de corpo livre porque não é uma força exercida sobre dele.

Cada ponta da corda exerce uma força de tensão sobre ele. Se assumirmos que a corda não tem massa e ignorando o atrito entre a corda e a ramifiação, então a magnitude da tensão é a mesma em toda a corda.

Porque o homem puxa para baixo na extremidade livre intencionalmente e em a outra extremidade sem querer (porque está amarrada em torno de sua cintura), a terceira lei de Newton prevê que ambas as pontas da corda o puxem para cima.

A terceira lei também prevê que a extremidade livre da corda puxa o homem com uma força exatamente igual da magnitude àquela da força de tração de .

Assim, além da força descendente gravitacional, existem duas forças de tensão para cima com magnitudes atuando no homem, conforme ilustrado no diagrama de corpo livre.

Tomando a direção positiva como para cima, e aplicando a segunda lei de Newton temos que

Resolvendo para a aceleração: