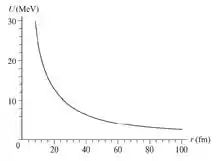
Imagine um núcleo de como uma combinação de uma partícula alfa () e um núcleo residual (). Faça um gráfico a partir da energia potencial eletrostática em função de , em que é a distância entre as duas partículas, para . Compare o resultado com a Fig. 42-10.
Passo 1
A energia potencial eletrostática é dado pela seguinte expressão:
Passo 2
As cargas da parícula alfa e do núcleo residual são respectivamente:
Passo 3
A constante vale , então a energia potencial (em joules) em função de (em metros) é:
E em eletronvolts (é só dividir por ) temos:
E se colocarmos em , temos:
Passo 4
Agora com a ajuda de um gerador gráfico, temos que a curva por para para é:
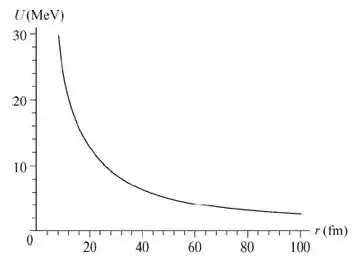
Resposta