Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 23

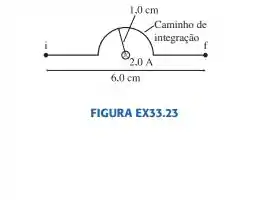
Qual é a integral de linha de B → entre os pontos i e f da FIGURA EX33.23?

Passo 1

Faaaaaala, galera... Tranquileba??

Sabemos que pela lei de Ampere:

∮ B → ∙ d S → = μ 0   I a t r a v é s

Onde temos tem caminhos em um, isto é: da esquerda ao semi circulo (ESC), o semi círculo (SC) e a direita do semi circulo (DSC). De forma que:

∮ E S C B → ∙ d S → + ∮ S C B → ∙ d S → + ∮ D S C B → ∙ d S →

Veja que a corrente está passando justamente centrica ao semi círculo, criando assim um campo magnético tangencial. De forma que:

B E S C ⊥ S E S C ;     B D S C ⊥ S D S C

E sendo perpendulares, sabemos que:

B → ∙ d S → = B * d S cos ⁡ θ ,   s e   B ⊥ d S ∴ B * d S * cos ⁡ 90 ° = 0

Sobrando somente:

∮ B → ∙ d S → = ∮ S C B → ∙ d S → = μ 0   I a t r a v é s

Passo 2

Assim:

∮ S C B → ∙ d S → = μ 0 I 2 π d     ( π d )

Note que, se feita integral, este será o resultado.

E ( π d ) é o comprimento do semi circulo.

Assim:

∮ S C B → ∙ d S → = μ 0 I 2

Passo 3

Aplicando valores:

∮ S C B → ∙ d S → = μ 0 I 2

∮ S C B → ∙ d S → = 4 π × 10 - 7 T m A 2,0   A 2   = 1.26 × 10 - 6   T   m

Resposta

∮ S C B → ∙ d S → = 1.26 × 10 - 6   T   m

Ver Outros Exercícios desse livro